Sammy001
Student
- Jan 19, 2021
- 8
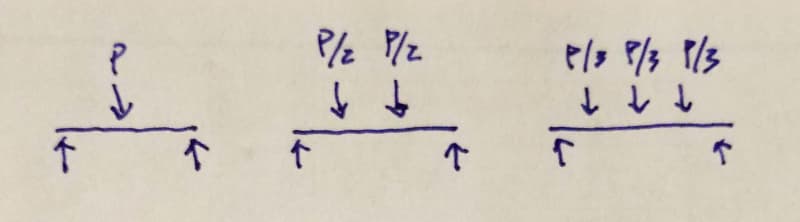
Does anyone know which beam has the highest moment for the same length? Is there a formula for multiple point loads?

Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
