Rocketman41
Mechanical
Conditions:
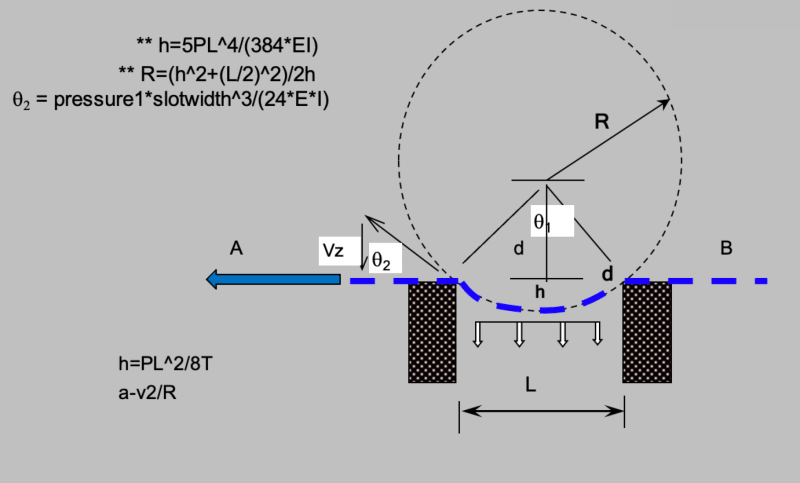
Impervious fabric pre-tensioned at (T pli) and over a vacuum slot (L in) wide
NEED:
Def(h) as a function of Slot width (L), Vacuum (V ), and pre-tension (P).
Note: I am familiar with the beam equations below but, none of them apply. see diagram below.
** h=5PL^4/(384*EI)
** R=(h^2+(L/2)^2)/2h
Angle of deflection the fabric (beam) makes = pressure1*slotwidth^3/(24*E*I)
Impervious fabric pre-tensioned at (T pli) and over a vacuum slot (L in) wide
NEED:
Def(h) as a function of Slot width (L), Vacuum (V ), and pre-tension (P).
Note: I am familiar with the beam equations below but, none of them apply. see diagram below.
** h=5PL^4/(384*EI)
** R=(h^2+(L/2)^2)/2h
Angle of deflection the fabric (beam) makes = pressure1*slotwidth^3/(24*E*I)

