Need help with understanding "Force method of analysis" in 2 dimensions 2

[Norbert_G]

Hi, first time posting here so I hope i don't break any rules and post in correct section. I have an exam soon and my prof failed to provide me with any sense-making answer (he constantly makes mistake when writing on the whiteboard meaning most of my notes are useless). I have an issue with understanding how to use force method when I add another dimension. On attached pic you can see 2 beams that are placed on eachother but without any welding. When calculating the missing force x1 do I treat it as if it was just another support for the beam called (1.) or do I need to also include the other beam (2.) into the equation?

 

[rb1957]

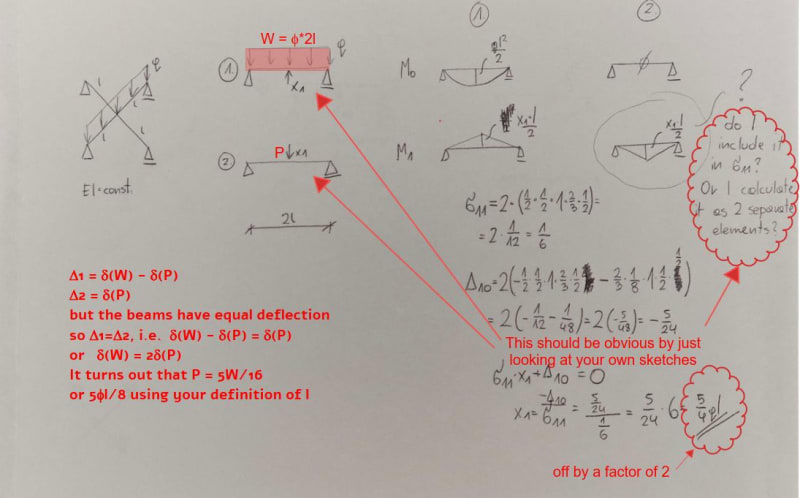
ok ... lets call the loaded beam "beam1" and the supporting beam "beam2".

In the typical problem the "crossing point" (where beam2 supports beam1) would be a fixed point, so your problem solution would be ...
a)remove the redundant support, and solve the beam1 statically, determining the deflection at the redundant point, D
b)solve beam1 for the unit load, calculating the unit deflection at the redundant point, d.
c)determine the redundant load, so that there is zero deflection at the redundant point = D/d (the equation here is (D/d)*d-D = 0 ... clear as mud?)

In this case there is some deflection at the redundant point, so
a) solve beam1 (without beam2) statically, determine the deflection at the redundant point, D.
b) apply a unit load to beam1, determine the deflection at the redundant point, d1.
c) apply a unit load to beam2, determine the deflection at the redundant point, d2 (in this case = d1).
d) then the deflection of beam 1 = deflection of beam 2 ... D-X*d1 = X*d2 ... X = D/(d1+d2)

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[BAretired]

I have an exam soon and my prof failed to provide me with any sense-making answer (he constantly makes mistake when writing on the whiteboard meaning most of my notes are useless).

Have a heart Norbert. It's easy to get confused, standing at the front of the class writing on the board.
If your notes are anything like your post, there is room for improvement, but it isn't rocket science; a little thought should bring you to a full and accurate understanding of deflection theory of two beams sharing a load.

 

[Norbert_G]

I don't know how to reply here so I'll just write like this. Sorry about Sh*ting on my prof, I just got frustrated for not being able to comprehend this normal way but thanks to both of your explanations I think I'm getting a hang of it! As for notations, these are specific for my country I suppose and may differ for you, that's why I decided to write here cuz I had no idea how to even look for an answer for that myself. Now I can pracitce it further with newly gained knowledge. Thanks again, you two were great help and I hope you have a great day

 

[rb1957]

have you tried google ? Unit Force Method, or force method, is a very standard solution, written up in countless texts.

What text are you using ?

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Norbert_G]

English is not my first language so I don't know all the specific terminology, tbf I didn't even know how to call these 2, let alone anything that resembles methodology specific to my Uni. That's why I opted to come here and I'm glad I did cuz I just passed my final with a A for that. I was hesitant at first because things you wrote aren't exactly written the same way my prof would write them but he accepted it since it was just slight variation of our methodology. Thanks again for help.

 

[rb1957]

ok, but I used your description "Force Method" (that I know as the Unit Force Method) ... did you try googling that ?

Also, this method is described in many texts (and probably many YouTube videos) ... what text are you using ?

But I'm curious ... if my description of the method isn't what your prof taught, what did he teach ??

"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Norbert_G]

I wasn't having an issue with finding what is a Force Method since I already knew how to use it in standard beams and frames. Problem arose when I had to look for a system such as these two. First translation that comes up for these is "grates" and "grids" which only started showing some 2D frames, not my specific use case where forces are perpendicular to each beam in the system. In my mother tongue most sources were pay-walled so no go either. Remember that google searches even when using english are still filtered by your location. As for what my prof taught us. The problem is he "kinda just got into calculating things". I'm the type of person who doesn't want just the formula, I need to know the process behind it and like I said, since a lot of my notes were riddled with sneaky mistakes (not intentional, I know) I had hard time deducing what's what on my own. I was mostly confused by the "they have equal deflection", my thought process was that since there's 2 of them in this specific point of declection then surely them together must provide more resistance than just one and I was looking for some magical "coefficient" but turns out it wasn't that complicated. And also, the language barrier played a role here as translators rarely work perfectly when it comes to field specific naming schemes.

 

[Woun1998]

I once had a similar task, and I remember spending a lot of time on it. Removing the unnecessary support and conducting a static analysis of beam1 is done to ascertain the deflection at the fixed point, referred to as D. Further examination involves analyzing beam1 under a unit load to compute the unit deflection at the fixed point, labeled as d. The goal is to determine a redundant load that results in zero deflection at the fixed point, expressed as D/d. However, the clarity of this determination may pose challenges, given the equation (D/d)*d - D = 0.
In instances where there is deflection at the fixed point, the process involves statically solving beam1 (excluding beam2) to establish the deflection at the fixed point, denoted as D. Subsequently, applying a unit load to beam1 yields the deflection at the fixed point, denoted as d1. Similarly, applying a unit load to beam2 and determining the deflection at the fixed point, denoted as d2 (which, in this scenario, is equal to d1). The relationship between the deflections of beam1 and beam2 is then expressed as D - X * d1 = X * d2, where X is calculated as D / (d1 + d2).
You don't have to apologize for your English, it's perfectly normal to not understand complex terms in a foreign language. I used to listen to lectures in French and many terms were similar, but they were difficult to understand. I would recommend looking for dictionaries or collections with scientific vocabulary, or trying to work on the language yourself or I would rather recommend asking for help for example

https://ca.edubirdie.com/english-help

or find a person who is fluent enough to help you. Nowadays, there are plenty of materials for self-study for various purposes. One of my friends lives in France, he speaks English well, but he had to take a separate English course for engineers, so it's okay not to understand something