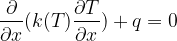Hello everyone.
I'm trying to describe Abaqus solver for my masters thesis, more exactly, for problem of heat conduction in solid, with temperature dependent thermal conductivity (k=k(T)).
I would like to derive the formulas from the ground up (see bottom picture), with example of a simple truss (1D). For start, I would work with steady-state problem and later upgrade to transient. I realize, that this is a non-linear problem, and am aware how Abaqus solves plastic deformation (Newton-Raphson alghoritm).
I have basically turned around google and google scholar, but all i find are books that are too general (FE), have to do with plasticity or articles that are too specific.
I am almost desperate at this point, so I'm asking this community to please give me some hint or maybe some literature for solving heat conduction with k = k(T).
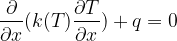
I'm trying to describe Abaqus solver for my masters thesis, more exactly, for problem of heat conduction in solid, with temperature dependent thermal conductivity (k=k(T)).
I would like to derive the formulas from the ground up (see bottom picture), with example of a simple truss (1D). For start, I would work with steady-state problem and later upgrade to transient. I realize, that this is a non-linear problem, and am aware how Abaqus solves plastic deformation (Newton-Raphson alghoritm).
I have basically turned around google and google scholar, but all i find are books that are too general (FE), have to do with plasticity or articles that are too specific.
I am almost desperate at this point, so I'm asking this community to please give me some hint or maybe some literature for solving heat conduction with k = k(T).