srm01
Structural
- Apr 6, 2022
- 10
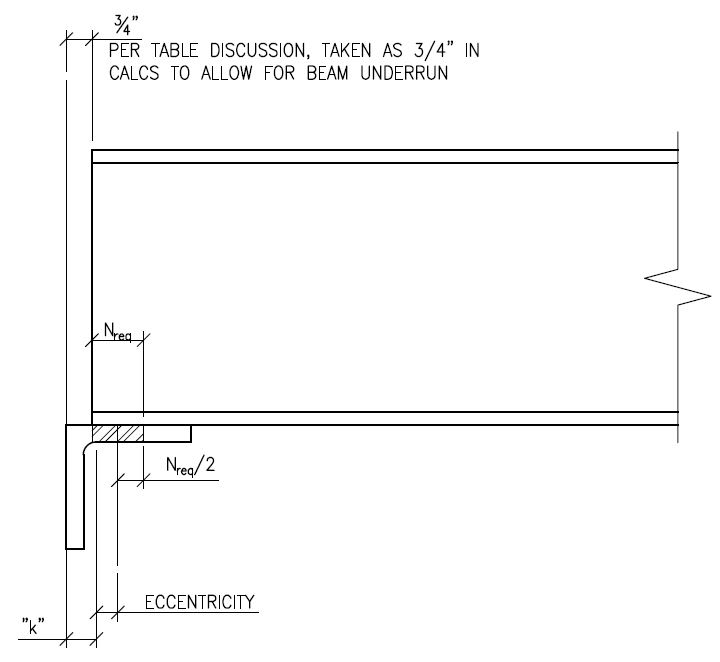
thread507-419698 just wanted to follow up on this thread. There is an equation for Nreq in Blodgett's Design of Welded Structures book. Page 5.2-2 equation (2): N = R/(t_w*(0.75*sigma_y))-K
Do you think that equation is valid for Table 10-6?
Do you think that equation is valid for Table 10-6?