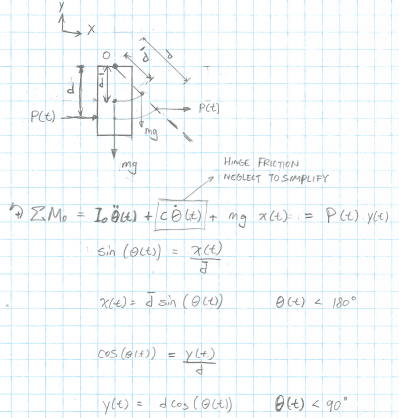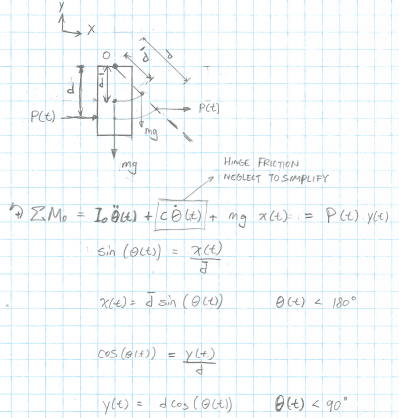Hi, I was interested to see this because I use a method here to solve similar 2nd ODE for power electronics,
transient electromagnetic and transient thermal applications.
The approach dates back 50 years when analog computers had patch panels .
Users would draw a block diagram just by inspection of the ODE and its auxiliaries, ready to patch it up.
Analog computers are extinct, but I found the block diagram method to be quick and useful.
I also use circuit simulators and FEM suite , but found some applications are better solved using this method.
The hardware is replaced by coding the function blocks (in this example,Python3).
Although the old analog computers could not solve a Partial DE (PDE),
I have used a similar method to solve PDE by equating (for example) a spatial finite differencing to an integrator in time.
The screenshots below are shown just as an example of the method using an approximate interpretation of MegaStructure's diagram.
Constants and initial conditions are not correct.
Block Diagram from ODE and aux functions.:
Python:
Results: