FerriteAlpha
Civil/Environmental
Hello everyone,
Yesterday I experimented a little bit with abaqus in order to understand different constraints. I noticed, that the numerical solutions for a simple model are very different to the results that I expected.
I created a VERY short column with an I-Shape cross-section. Now, since the column is so short that buckling doesn't occur, I expect the axial resistance to be N=A*fy, where A is the area of the cross-section and fy is the strength of the material. In this case I used a simple ideally plastic behaviour of a S235 steel (fy=23.5kN/cm²).
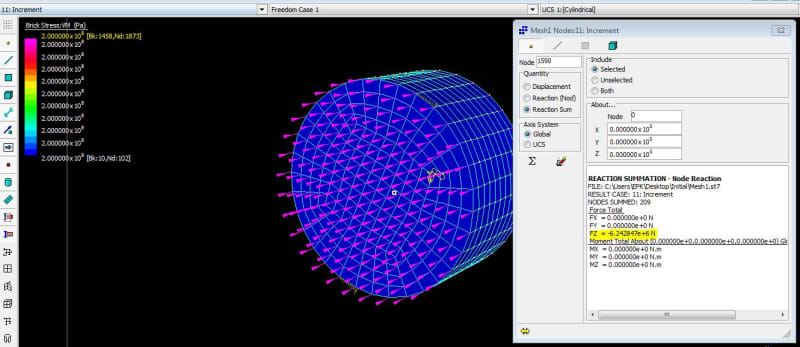
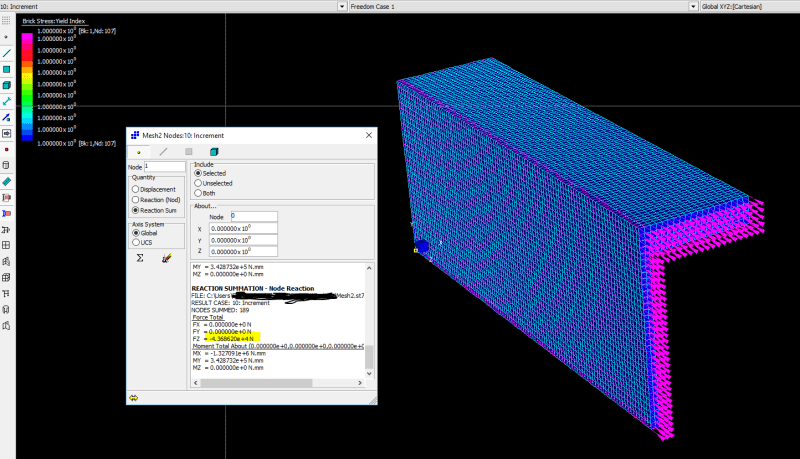
The cross-sectional area of my attached model (if the area is duplicated, since only one half is modelled) is around A=744mm²=7.44cm². Therefore the analytical plastic axial force is N=7.44*23.5kN/cm²=175kN. Creating the model with S4 elements leads to the right solution. With the model in the attached input-file I get around 120kN (duplicated Reaction force). So it is far too low. On the other hand I created the whole cross-section with C3D8R elements without using the symmetry plane. Then the axial force was around 200kN. So it was too high. I am honestly very confused. I'm not sure if its because of the boundary conditions or constraints or something else... I just can't figure it out...
It would be great if someone could help me out with this one.
Yesterday I experimented a little bit with abaqus in order to understand different constraints. I noticed, that the numerical solutions for a simple model are very different to the results that I expected.
I created a VERY short column with an I-Shape cross-section. Now, since the column is so short that buckling doesn't occur, I expect the axial resistance to be N=A*fy, where A is the area of the cross-section and fy is the strength of the material. In this case I used a simple ideally plastic behaviour of a S235 steel (fy=23.5kN/cm²).
The cross-sectional area of my attached model (if the area is duplicated, since only one half is modelled) is around A=744mm²=7.44cm². Therefore the analytical plastic axial force is N=7.44*23.5kN/cm²=175kN. Creating the model with S4 elements leads to the right solution. With the model in the attached input-file I get around 120kN (duplicated Reaction force). So it is far too low. On the other hand I created the whole cross-section with C3D8R elements without using the symmetry plane. Then the axial force was around 200kN. So it was too high. I am honestly very confused. I'm not sure if its because of the boundary conditions or constraints or something else... I just can't figure it out...
It would be great if someone could help me out with this one.