Belisario_G
Mechanical
Hi peeps,
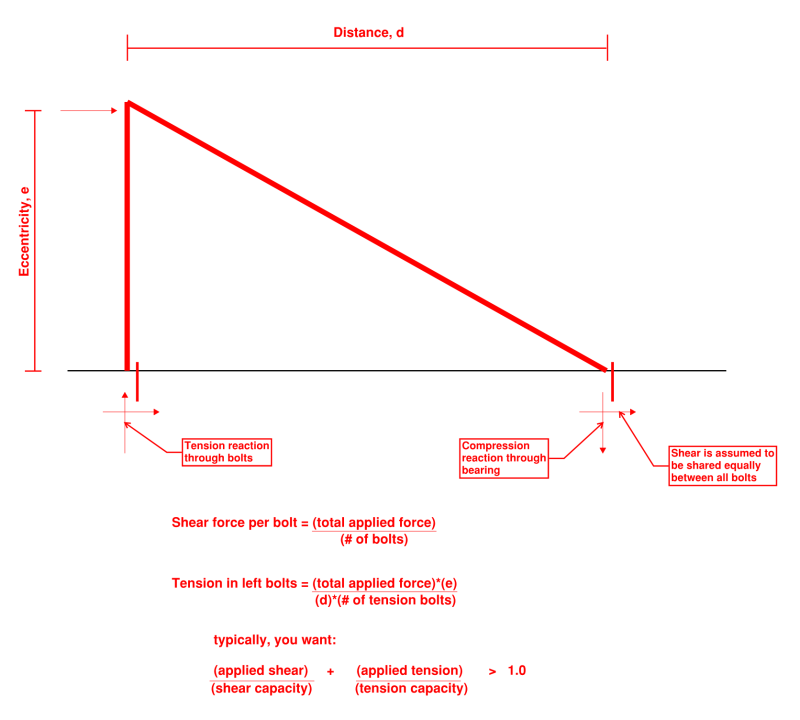
This frame will be bolted on the ground. The load applied is shown by the red arrow, my question is how to deal with this loading type. Can anyone recommend an analysis method for the bolts ? I know the bolts are undergoing shear force and bending moment (out-of plane), but I'm not familiar with real life approaches to this problem (Steel code etc.).
Attached are some views to this structure
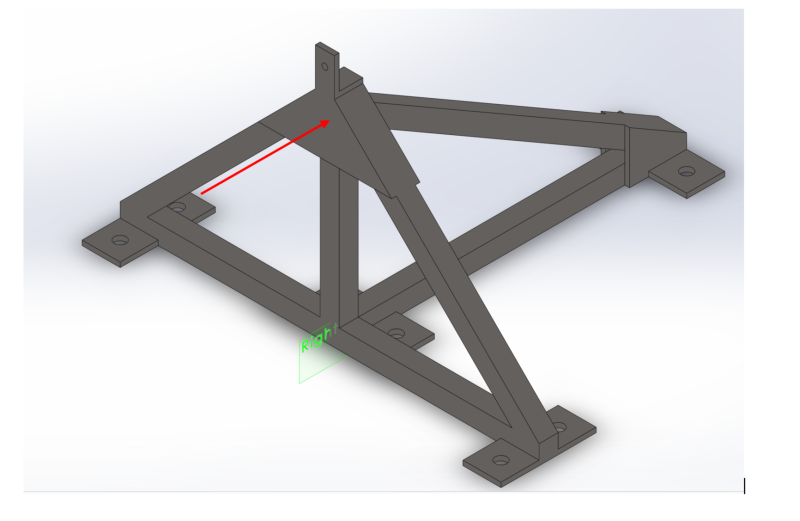
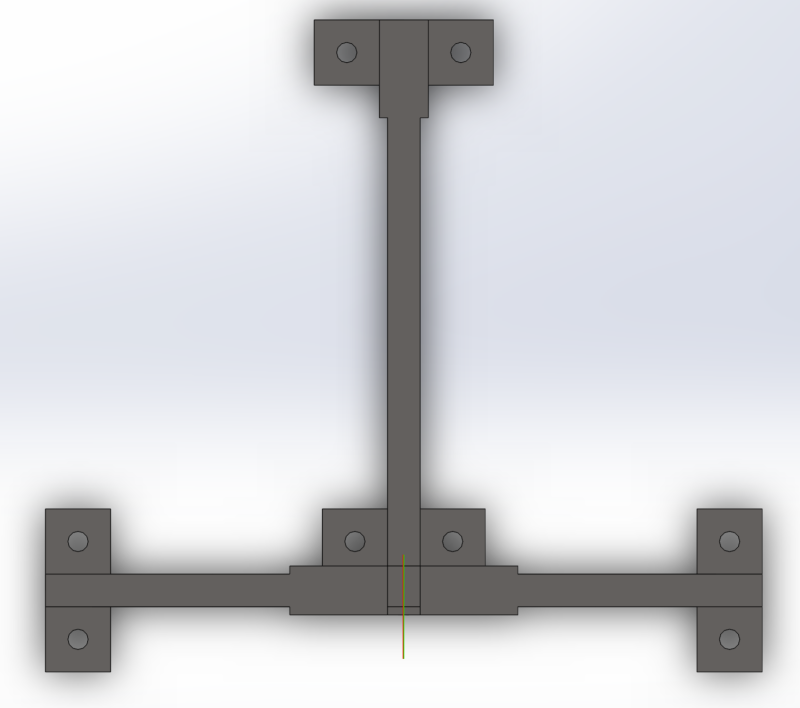
This frame will be bolted on the ground. The load applied is shown by the red arrow, my question is how to deal with this loading type. Can anyone recommend an analysis method for the bolts ? I know the bolts are undergoing shear force and bending moment (out-of plane), but I'm not familiar with real life approaches to this problem (Steel code etc.).
Attached are some views to this structure