Have you had any academic experience with energy methods?
Yes, but nothing more than the brief discussion of how work energy equations were derived. At this point I wouldn't be able to recreate the math involved to derive any of those principle equations or provide a coherent explanation of them. At best, I know how to determine deflections using the energy method of Virtual Work for trusses and beams. Even in this situation, I'll skip the integrals for beams and use a moment integral table to quickly look up some required values. As far as indeterminates, besides making safe assumptions or using computer analysis, I can apply some basics for Force Compatibility methods... and I cannot even remember if force compatibility is some derivative of the energy method...
Over my career I have found that when new information comes in, it will replace the shelf items that aren't in use. It's a maddening source of frustration, but with dwindling budgets and the need to accomplish a whole lot more responsibility with less time (the life factor), I find myself replacing these concepts with quicker ways to process the information and getting a job done efficiently.
I believe I'm at the point where most of my effort is put into 'good construction practice' as I can usually find a way to justify the design of all the elements that make the big picture. A personal goal of mine, and what I believe is the higher order of structural engineering, is understanding the stability of the system as a whole. Which is unfortunately difficult to do without the right project exposure, guidance, design example to follow, etc.. I find this particular topic much more difficult that designing any single components of a structure.
Those show up a lot in stability design, as well.
I will have to find more reading on the subject. I actually searched the text in multiple steel design textbooks I have for combinations of the words, "lower, bound, theorems" and got a handful of results that don't provide any information. I believe this subject is on the higher order of understanding that I mentioned earlier. These things are sometime easy to feel but hard to explain (like a good song). Stability is something you can feel from the age of stacking blocks... but explaining the non-linear response of a 2nd order analysis and why it's important to use reduced stiffnesses because a structure is within it's yield limit states... that's a doozy.
we've seen from research that a lot of the shear load goes into the top two bolts in a bolted connection, but we provide more and load them all equally "in design"
It's funny you bring this up because I've used this approach in many cast-in-place anchor situations before. Again, this was handled through a particular program calls "Studs" by STI. I will need to refresh myself on ACI's stance on the matter.
This engineering blog is a unique place where the people who care to know are mostly investing their own time to be here. My experience is that most individuals don't want to know, they just want a solution (which is fine). It's actually alarming to me that so many of my peers in the industry cannot hold much of a conversation when it comes to the stability chapter "C" in the AISC manual. Feels like they are relying on previous examples to know things will work.

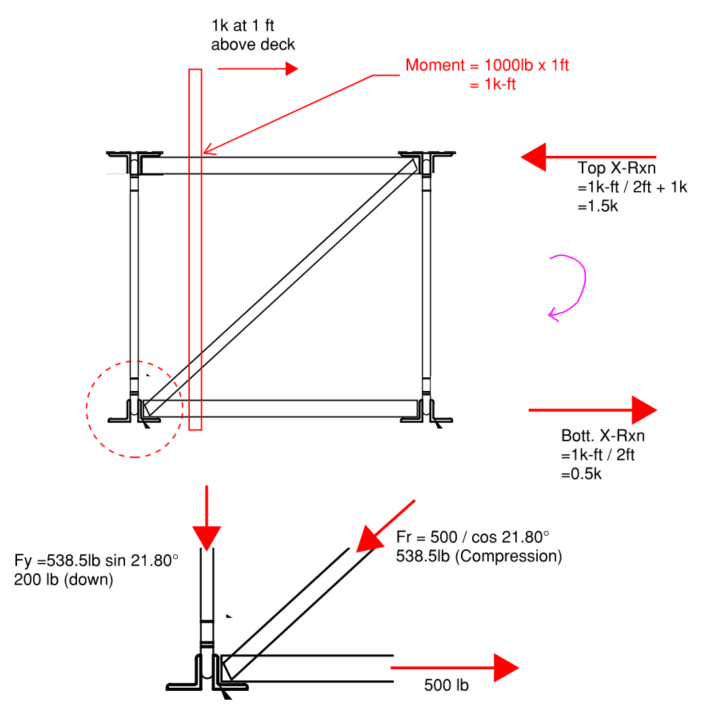
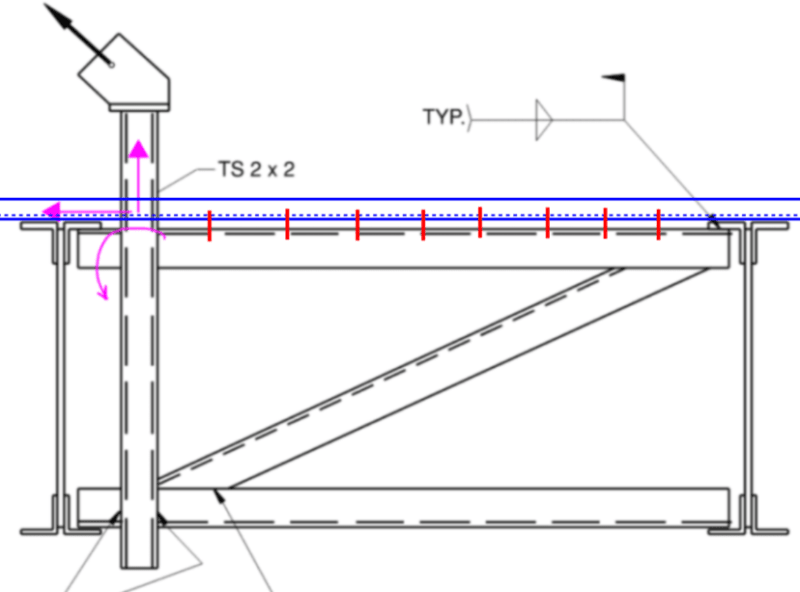
![[wink] [wink] [wink]](/data/assets/smilies/wink.gif)