PE Chemical Thermodynamics Questions

[AthlonXPme]

I have been scratching head on these two thermodynamics questions. Can anyone shed some lights ? These two questions are all related to phase equilibrium.

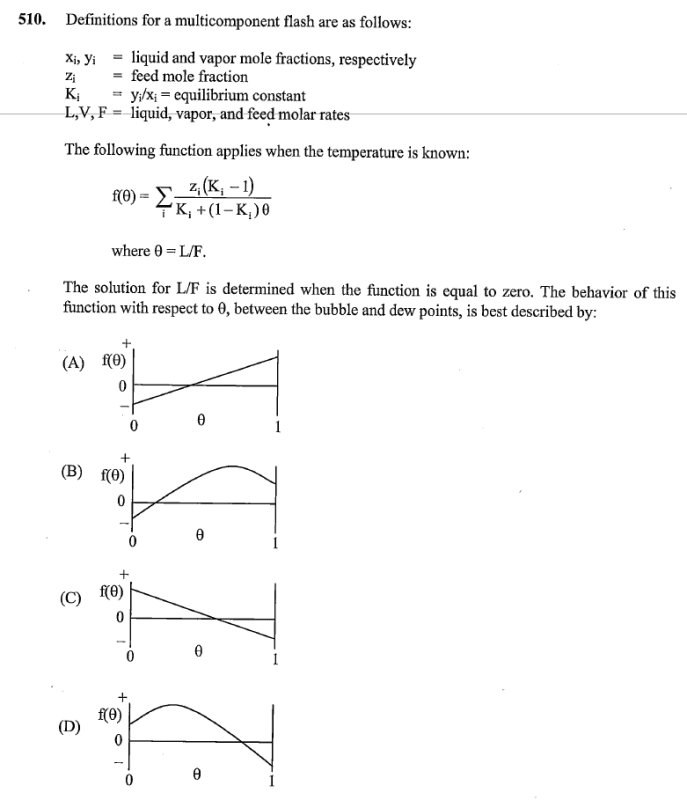
PE Reference:

 

[IRstuff]

Home problems should be posted in the Student Forum

TTFN (ta ta for now)
I can do absolutely anything. I'm an expert!

https://www.youtube.com/watch?v=BKorP55Aqvg

faq731-376 forum1529 Entire Forum list

http://www.eng-tips.com/forumlist.cfm

 

[georgeverghese]

The term z in these questions is not well described. Context to these questions is in Perry Chem Engg Handbook 7th edn Chapter 13, section on Single Stage Flash Calcs, where z is described. Answers will then be obvious.

 

[AthlonXPme]

@georgeverghese
Thank you for the direction. I believe here is the reference you were referring to. With this, I am still having hard time to solve these two problems. Can you explain in details ?

 

[TiCl4]

IRStuff,

Normally, I agree. However, PE licensing is not a "Student" issue - it is a matter of a practicing engineer that is pushing for a professional license.

The only other possibly appropriate forum is "How to Improve Myself".

 

[Latexman]

AthlonXPme,

In that same chapter of Perry's, find the section on "Prediction of K Values". You should find some DePriester graphs of K's for hydrocarbon systems. Pick a component, and develop a general understanding of how K behaves with constant P and rising or falling temperature. You should learn that K at constant pressure increases with temperature. Then, use that knowledge along with the sections you posted above to rationalize the answer to problem 509.

Good Luck,
Latexman

 

[AthlonXPme]

@Latexman
Thank you providing the guidance.
The answer is D if I am correct. At bubble point, Sum (KiZi) =1. At dew point, Sum (Zi/ki) = 1. Within the two phase means the temp is between bubble point and dew point temps. Thus, both Sum (KiZi) and Sum (Zi/Ki) is greater than 1.
Do you have any idea about problem 510 ?

 

[Latexman]

@AthlonXPme
We know that T[sub]BP[/sub] < T[sub]DP[/sub]. Let's take them from lowest to highest.
At T[sub]BP[/sub] Sum(KiZi) = 1. If we raise T above T[sub]BP[/sub] Ki's will increase and Sum(KiZi) > 1.
At T[sub]DP[/sub] Sum(Zi/Ki) = 1. If we lower T below T[sub]DP[/sub] Ki's will decrease and Sum(Zi/Ki) > 1.
I agree, both Sum (KiZi) and Sum (Zi/Ki) is greater than 1, so the answer is D.

Good Luck,
Latexman

 

[georgeverghese]

Hints to solving 510:
a) When theta = 0, we have dewpoint; when theta = 1, we have bubble point. So temp is decreasing as you move down the x axis, and so K decreases for each component also, for non regular azeotropic behaviour
b) The expression for f(theta) can be teased out, with a little algebra on the PE reference 3.6.6.3, as being equal to Sum(y_i) - Sum(x_i). This is also the converse of equation 13-14 in Perry

 

[AthlonXPme]

@georgeverghese
Since K decreases when moving down the X axis, should f(theta) decrease as well so that answer is either C or D ? How to pick between C and D ?
If f(theta) = Sum (y_i) - Sum (x_i), then f(theta) is always zero ?
I need more hints.

 

[pierreick]

Hi,
Consider this tutorial to support your studies.

https://www.e-education.psu.edu/png520/m12.html

All the best
Pierre

 

[georgeverghese]

The y axis can be viewed as a residual error term. Solution is reached when the iteration value for theta results in y=0.
To see which of these curves matches our observations, we find the first derivative of this residual

Rewrite this expression as y = Sum [a(c-1)/(b +(1-c)x)], where x = theta; c = K_i, which is always positive

dy/d(theta) = Sum [a.(c-1). -(1/(b+(1-c)x))^2 .(1-c)]
or
dy = Sum [+a.((1-c)^2).(1/(b+(1-c)x))^2] . d(theta) -equation 1


d (theta) is the (next iteration value of theta, at which point the expected value of y is 0) - (current value of theta)

There is no local inflexion, and the slope of this line is always +ve.

The closest to these trends is A

It would be possible to use eqn 1 in a Newton Raphson type accelerated search algorithm to derive the next iteration value for theta if you were to write out a program to speed up convergence, as stated in Perry's Handbook.

 

[pierreick]

Hi,
Agree with George, derivative f{teta)is always positive.
y'= sum (zi*(ki-1) ^2/ ((ki-1) *(1-teta) +1) ^2 >0
y" cannot be zero.
answer should be A
Pierre

 

[AthlonXPme]

@georgeverghese @pierreick
Thank you both for the explanation. Did not expect this needs some math skills to obtain the first order derivative. The answer A makes total sense !