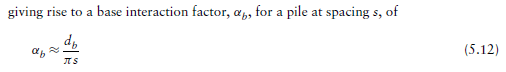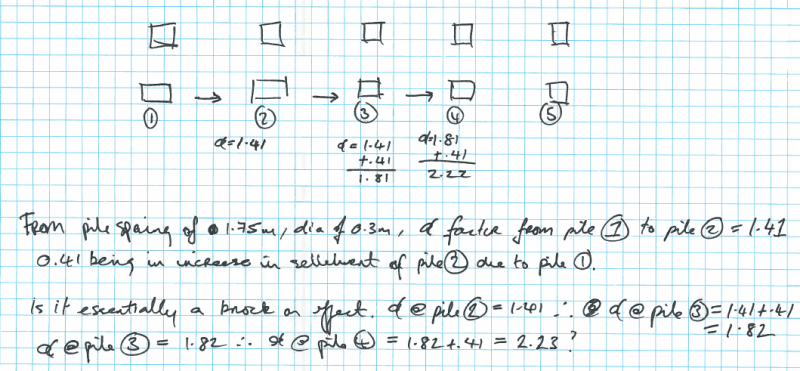UP830
Civil/Environmental
- May 18, 2018
- 15
Hello,
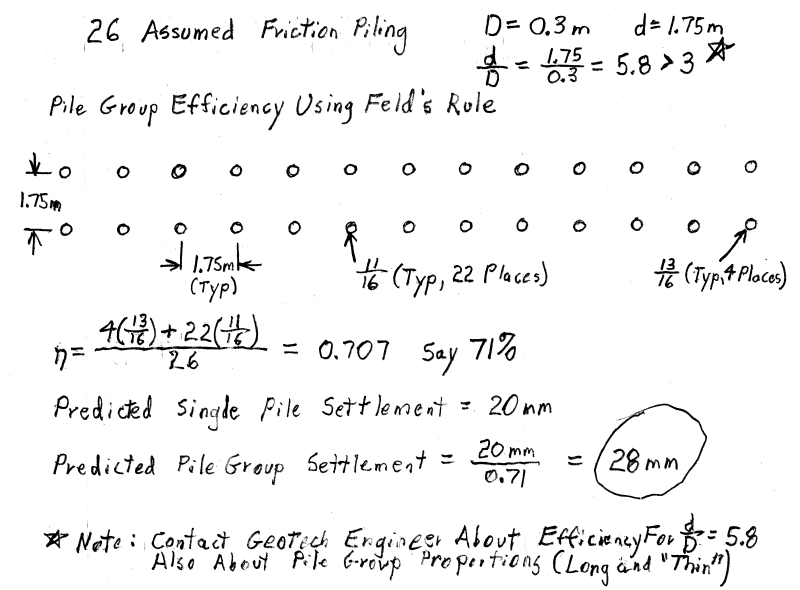
I am doing some independent learning of pile groups. Finding good resources for pile groups is hard in my opinion. There only ever seems to be a page or two on pile groups in most text books. If anyone has some good references for pile groups could they please comment.
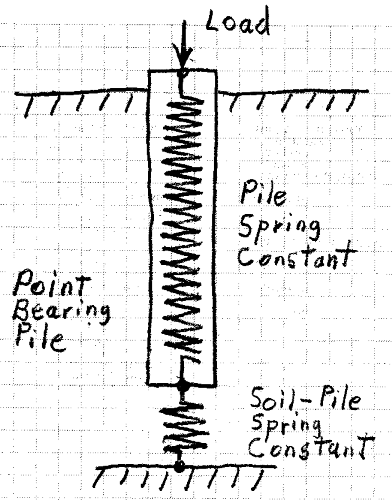
Also, could someone tell me where the below formulae for pile spring stiffness comes from? I have searched and searched and searched and have not found it. Or, if you have another pile spring stiffness formulae, please let me know its reference.

Thank you.
I am doing some independent learning of pile groups. Finding good resources for pile groups is hard in my opinion. There only ever seems to be a page or two on pile groups in most text books. If anyone has some good references for pile groups could they please comment.
Also, could someone tell me where the below formulae for pile spring stiffness comes from? I have searched and searched and searched and have not found it. Or, if you have another pile spring stiffness formulae, please let me know its reference.

Thank you.



![[idea] [idea] [idea]](/data/assets/smilies/idea.gif)
![[r2d2] [r2d2] [r2d2]](/data/assets/smilies/r2d2.gif)