Plastic Moment of resistance of beam with welded tee at bottom 2

[ajk1]

Does anyone know of software that will calculate the plastic moment of resistance of a steel beam with welded Tee section at the bottom? I started writing a spreadsheet, but is a little laborious to cover all cases because the PNA can fall above the bottom flange of the beam, below the bottom flange of the beam or within the bottom flange of the beam.

 

[ajk1]

Thank you Kootk and BAretired for all the time and effort that you have spent on this. Your latest messages about it are what I would have thought was the case, i.e. using all the welds to develop the fyAs each side of the location of maximum moment, although most of my work has been in concrete more than steel. It seems to me that this is similar to cover plates which was in the old CSA S16 Standard which I have handy (but I am not sure that it is in the current S16) and sets out the design parameters quite clearly, although not for LSD. I don't see there though anything for Tees with respect to the end length of a', so presumably requirements about relating the size of the welds near the end to the thickness etc. of other member are required only for cover plates.

I will print out Kootk's latest message and study it more. Looks quite comprehensive.

 

[KootK]

I don't see there though anything for Tees with respect to the end length of a'

Yeah, I think that it's just like cover plate theory with the a' stuff replaced by the tension/shear lag bit that we discussed above.

It seems to make sense to determine the total length of full penetration weld required to resist As.Fy of the tee, then to provide that length in an intermittent weld with weld segments spaced equally each side of the maximum moment (assuming uniform load).

This strategy would require the more heavily loaded welds to yield and redistribute load to the more lightly loaded welds. How to we feel about that aspect of it? I've always thought of welds as not being very ductile. But then most welded connections require some degree of redistribution capacity in order to function as designed. AISC has a 1.25 factor that is applied to non-uniformly loaded welds of a different sort. I'd be tempted to apply it to this strategy as well.


I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[ajk1]

Kootk - I am not following. You seem to be summing the shear force over the unreinforced length from the end of the reinforcing tee to the end of the beam, to determine the weld near the end of the tee. Why would that be?

 

[KootK]

You seem to be summing the shear force over the unreinforced length from the end of the reinforcing tee to the end of the beam, to determine the weld near the end of the tee. Why would that be?

That's exactly right ajk1. Graphically and physically, that's what MQ/I "is". Think of it this way:

1) if you extended your reinforcing full length and specified a ridiculous weld spacing that perfectly matched shear flow demand, you would have just enough weld to develop the force in the reinforcing on either side of the peak moment location. The math just works out that way.

2) if you now cut the reinforcement short and leave the welds as they were, your total weld capacity would now fall short of being able to develop the required force in the reinforcing. And the shortfall would be exactly equal to the shear flow demand that would have otherwise been present between the end of the reinforcing and the end of the member.

3) The MQ/I-ish termination welds represent the reinstatement of the shortfall described in #2.

I'd like to revise my "what to do" recommendations to this:

1) Do VQ/I along the length.
2) Do MQ/I at the ends if partial length.
3) Do the tension lag extension that we discussed.

This strategy will be simple, reasonably efficient, and conservative for all cases where section plasticity is involved. And the requirement to fully develop the peak flange force will be automatically satisfied.

I've come to feel that developing As x Fy uniformly may not be the best way to go. That strategy would make the full, reinforced section available to you at the location of peak moment demand but, possibly, nowhere else. Presumably, you want the extra strength and stiffness available to you along much of the length of the member. For that assumption to be valid, I believe that the reinforcing section needs to be developed for MQ/I-ish forces beyond the theoretical cutoff points.



I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[MJB315]

I'm with you Kootk. Develop the WT (or cover plate) with enough welds on each end and then size the stitch welds for the shear flow / unbraced length (compression plates).

A lot of piece of mind for a little extra weld.





"We shape our buildings, thereafter they shape us." -WSC

 

[ajk1]

Thanks Kootk for a clear point by point description. Much appreciated. I am not sure why the end weld has to develop all the shear in the length of unreinforced beam beyond the reinforcing plate. We don't do that when the bottom bars in a concrete beam are terminated short of the beam end...or do we? I'll check the Code. Anyway, I am not doubting what you say, I just need to do some thinking to understand it.

Thanks MJB35. That is almost always my approach...be conservative. Then can sleep better at night.

 

[KootK]

Anyway, I am not doubting what you say

Oh no, doubt it. I figured out much of it during the course of this thread.

We don't do that when the bottom bars in a concrete beam are terminated short of the beam end...or do we?

Interesting observation. I would argue that for both the steel and concrete scenarios, the following is true:

1) Where the extra reinforcing is first introduced (theoretical cutoff point), you need to quickly develop it for the portion of the flexural tensile demand that the reinforcing is assumed to be dealing with at that location.

2) The demand in #1 is based on the moment demand at the theoretical cutoff point.

3) The moment demand at the theoretical cutoff point is the integral of [applied shear x lever arm] up to the theoretical cutoff point.

4) If you connect the dots (1->2->3), I think it reasonable that reinforcing termination development is a function of the shear from the end of the reinforcing to the end of the reinforced member.




I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

I can't agree with point (4) above. Reinforcement development is a matter of developing enough bond to provide adequate tension in the bar where it is required. It has nothing to do with shear occurring beyond the added reinforcement.

BA

 

[BAretired]

Is there anything wrong with using VQ/I throughout the reinforced portion of the beam in order to determine the amount of weld required at every section?



BA

 

[KootK]

I can't agree with point (4) above. Reinforcement development is a matter of developing enough bond to provide adequate tension in the bar where it is required. It has nothing to do with shear occurring beyond the added reinforcement.

I stand firm on this one. Try another version on for size:

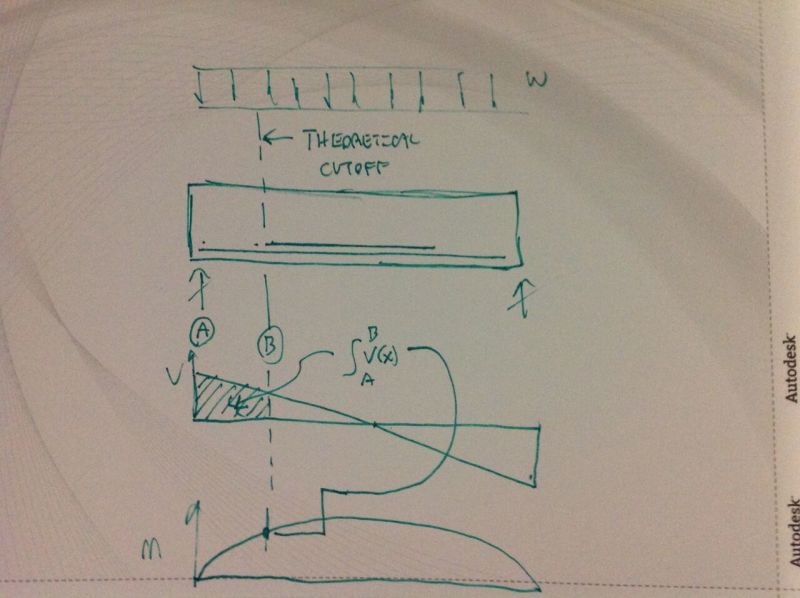
1) Required bond is a function of required flexural tension demand at the point of theoretical cutoff (B below).

2) Required flexural tension is a function of the moment demand at the section associated with theoretical cutoff.

3) The moment demand associated with the theoretical cutoff location is a function of the aggregate shear from A to B below. Literally: M = INT(V(x))|A-->B.

If one agrees with points one through three, then one would have to conclude that required rebar development is a function of the summed shear demand from A to B which is analogous to MQ/I in our steel reinforcement problem.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

Is there anything wrong with using VQ/I throughout the reinforced portion of the beam in order to determine the amount of weld required at every section?

Yes, for partial length reinforcing scenarios, I believe that there would be something wrong with it.

If the reinforcing extended full length and one provided exactly VQ/I the whole way, then the aggregate horizontal shear transfer capacity would exactly balance the force demand in the reinforcement at the location of peak moment.

If you cut the reinforcement short, and the horizontal shear attachment along with it, then you would not have enough aggregate shear transfer capacity to balance the force demand in the reinforcement at the location of peak moment. The shortfall would be MQ/I.

The above pertains to an elastic system but the same logic would hold were plastic section capacity required.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

Referring to your sketch above, I would have said that the theoretical cutoff is the point where the full length reinforcement is just capable of resisting the moment Mb by itself. Beyond that point, additional reinforcement is needed to carry the surplus moment. Calling midspan point C, additional reinforcement is needed to carry Mc - Mb. In addition to that, however, the bars require a certain amount of development length outside the theoretical cutoff points.

The moment at any point x is equal to the area under the shear force diagram between the support and point x. That is not in question, but the amount of additional reinforcement is a function of the difference between maximum moment and the moment which the main reinforcement can resist on its own.

I don't think that is quite the same problem as we are discussing in this thread although there are similarities.

BA

 

[KootK]

I agree with all of that BA. However, your statements all reflect typical concrete design methodology. In order to make the concrete analogy that ajk1 tabled consistent with the steel reinforcing scenario, I had to take a different tack. Much of what good concrete detailing is revolves around paying attention to issues analogous to MQ/I. We're just so used to dealing with it in concrete that it's second nature.

but the amount of additional reinforcement is a function of the difference between maximum moment and the moment which the main reinforcement can resist on its own.

Calling midspan point C, additional reinforcement is needed to carry Mc - Mb

But Mc - Mb = Mc - INT(V(x))|A->B. So still dependent on the aggregate shear beyond the extent of the reinforcement.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

KootK,

The term "aggregate shear" is unfamiliar to me. What you are calling aggregate shear is in fact not shear at all. It is shear times distance with units of foot-pounds or kilo-Newton-meters. But if that is how you define aggregate shear, the additional reinforcement is carrying the aggregate shear defined by the area of the triangle between point B and midspan on your sketch and has nothing to do with the shaded area between points A and B.



BA

 

[BAretired]

In order to develop the full tension in the tee, the weld must resist As.Fy:

t.L.Fy/2 = As.Fy (this assumes the full pen weld strength is Fy/2)
so L = 2As/t

where t is the stem thickness of the tee and L is the total length of weld required

For a WT180x32
As = 4070 mm²
t = 7.7 mm
L = 2(4070)/7.7 = 1057 mm

If the length of tee is 8m, the half length is 4m and the average length of weld required is 264 mm/m. If we assume the same provisions as CSA S16 specifies for composite action (shear studs may be placed uniformly between the point of zero moment and the point of maximum moment) then we could use 110mm of full pen weld at 400 mm o/c.

Alternatively, recognizing that full pen welds are not as flexible as shear studs, if we want to ensure that the shear flow is adequate at every section, we should space our welds at 400 mm o/c and use a length of weld varying from 220 at the end down to 0 at midspan. Of course, some reasonable minimum would apply, say 50 or 75 mm.



BA

 

[KootK]

The term "aggregate shear" is unfamiliar to me. What you are calling aggregate shear is in fact not shear at all

.

By aggregate shear, I simply meant the area under the shear diagram. It was not the greatest choice of phrasing in retrospect. However, you seem to have interpreted my meaning perfectly and one gets a little tired or repeating the phrase area under the shear diagram over and over again.

But if that is how you define aggregate shear, the additional reinforcement is carrying the aggregate shear defined by the area of the triangle between point B and midspan on your sketch and has nothing to do with the shaded area between points A and B.

The area under the triangle from B to C does define:

1) the felexural tension demand in the cutoff bars at the location of peak demand (C) and;
2) the reinforcement development/anchorage required beyond that point.

For this analogy, however, I would argue that these things are not the parameters of interest. Rather, the parameter of interest is the demand for flexural tension development/anchorage past the theoretical bar cutoff points (B). And that is based on the portion of the moment at location B resisted by the cutoff bars and, by extension, the area under the shear diagram between points A and B.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

I am not sure why the end weld has to develop all the shear in the length of unreinforced beam beyond the reinforcing plate. We don't do that when the bottom bars in a concrete beam are terminated short of the beam end...or do we? I'll check the Code.

I believe this "check" to exist in CSA A23.3 in the code clause shown below where Mf would be the moment at the bar cutoff location. It's really a tough analogy to make in concrete because development in modern codes is complicated by all manner of extra stuff (tension lag, shear effects, etc). The parallels would have been easier to draw back in the bond stress days. Anyhow, here's how I see MQ/I playing out in concrete using the quoted code clause:

1) Sum the area under the shear diagram from the end of the member to the theoretical cutoff point to get Mf.
2) Use Mf/dv to get the flexural tension demand (Tf_tot) in all of the bars present at the theoretical cutoff point.
3) By ratio of bar areas, determine the flexural tension demand in just the bars being cutoff (Tf_co).
4) Ensure that the bars that are cutoff are developed/anchored for Tf_co beyond the theoretical cutoff point.

I believe that this establishes a clear chain connecting the required development of reinforcing bars beyond the theoretical cutoff point (#4) to the area under the shear diagram beyond the theoretical cutoff point (#1). Steps two and three, taken together, essentially do the job of Q/I which is to isolate the flexural stress in the connected "reinforcement" from that in the rest of the section.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

For this analogy, however, I would argue that these things are not the parameters of interest. Rather, the parameter of interest is the demand for flexural tension development/anchorage past the theoretical bar cutoff points (B). And that is based on the portion of the moment at location B resisted by the cutoff bars and, by extension, the area under the shear diagram between points A and B.

Perhaps we are defining the cutoff point in a different way. I say the cutoff point is the location where the full length reinforcement is just able to resist the moment by itself. Beyond that point, additional reinforcement is needed; thus there is no demand on the additional reinforcement at the cutoff point, but normal practice would be to extend the bars beyond the cutoff point for full or partial development.

If concentrated loads were added each end of the beam between points A and B, keeping the uniform load the same throughout, Mb would increase, creating greater demand on the full length reinforcement but the additional reinforcement would be unaffected by it because Mc - Mb would not change. There would still be no demand on the additional reinforcement at the theoretical cutoff point.




BA

 

[KootK]

Perhaps we are defining the cutoff point in a different way. I say the cutoff point is the location where the full length reinforcement is just able to resist the moment by itself.

No, we've been thinking of the same theoretical cutoff point BA.

thus there is no demand on the additional reinforcement at the cutoff point

If concentrated loads were added each end of the beam between points A and B, keeping the uniform load the same throughout, Mb would increase, creating greater demand on the full length reinforcement but the additional reinforcement would be unaffected by it because Mc - Mb would not change. There would still be no demand on the additional reinforcement at the theoretical cutoff point.

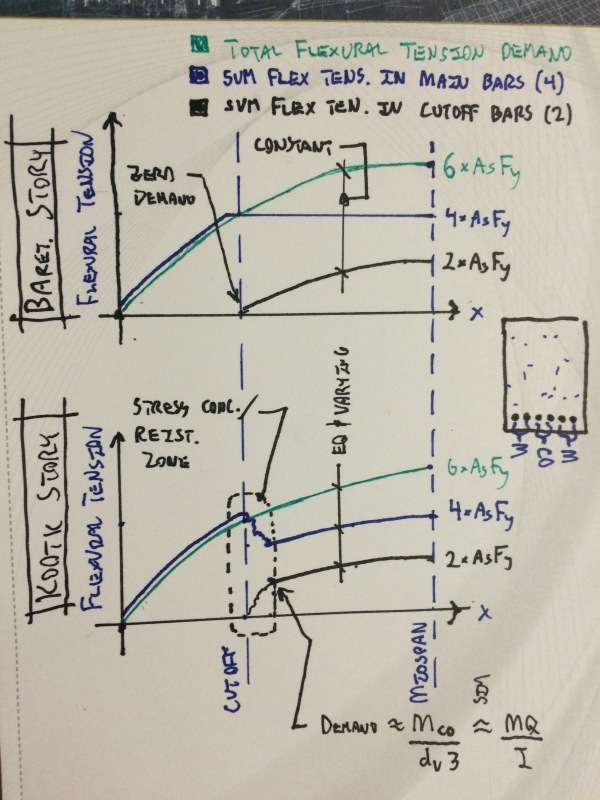
Based on the above statements, I believe that our difference of opinion stems from our telling two different stories regarding the flexural tension demand in the rebar at the cutoff locations. See my sketch below and let me know if it fails to accurately reflect your thinking.

With steel reinforcing of steel beams, the MQ/I story is saying that:

1) Immediately to the left of the theoretical cutoff point, all stresses are distributed in MC/I fashion throughout the unreinforced section and;
2) Immediately to the right of the theoretical cutoff point, all stresses are distributed in MC/I fashion throughout the reinforced section.

Making that pseudo-instantaneous jump is what creates the MQ/I and tension lag demands immediately beyond the cutoff point. My story of cutoff rebar flexural tension demand is consistent with the MQ/I philosophy. Your story is not. And that's not to say that my story is more correct than yours or, indeed, that my story is correct at all. Mine simply parallels MQ/I methodology. I also feel that my story is more compatible with strain compatibility (pun intended). But then, we assume strain compatibility in concrete in many instances where it clearly doesn't exist.

I've reviewed a few of the concrete textbooks that I have on hand with regard to this issue. All simply state that, for a number of reasons, bars should be extended beyond the theoretical cutoff point. And I don't dispute that will produce safe designs regardless of which of our stories more closely reflects the truth.

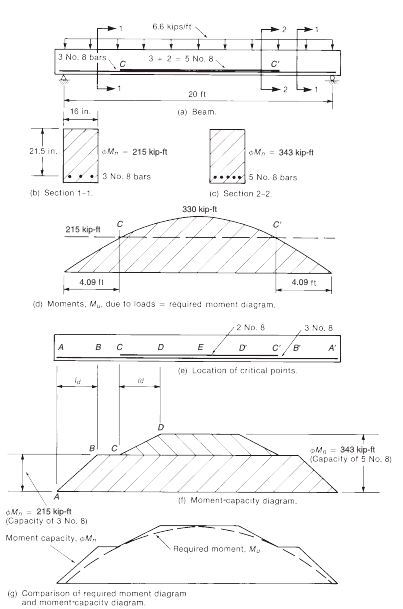
I was hoping that I could find something in print that would make one of our flexural tension demand stories the clear winner but, so far, I've come up empty handed. I've included MacGregor's version below for reference. It deals with overall, mobilizeable code capacity but doesn't say much regarding the expected stress in individual bars.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[BAretired]

I agree that the precise stress in the bars in the vicinity of the cutoff is not too clear, particularly when bars are terminated in a tension zone. For that reason, I tend to extend bars one development length beyond the theoretical cutoff point.

In the case of the WF reinforced with a WT, there is a similar problem. The stem and flange of the tee are by necessity, unstressed at the physical end of the tee. The flange is unstressed for some distance beyond that because of shear lag in the stem, so the prudent designer would take that into account when determining the length of the WT and would likely call for continuous weld in the portion beyond the cutoff point. That would be a matter of engineering judgment.

So far as the full penetration weld along the stem of the tee is concerned, I tend to agree with one of your earlier statements that to distribute the weld uniformly between the end of the tee and the point of maximum moment as we do for example with shear studs in composite beams, is not a prudent course of action because the welds are not as flexible as shear studs. For that reason, the weld metal should be distributed in a manner compatible with the shear flow along the stem of the tee.

BA