BAGW
Structural
- Jul 15, 2015
- 392
Hi,
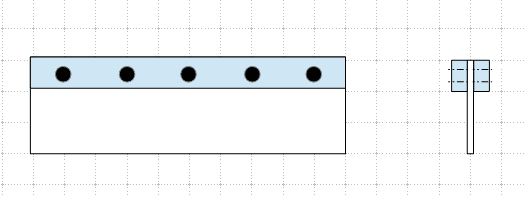
I have a question regarding the plug weld design. Per AISC the base metal have to be checked per section J4. When I am checking the shear rupture for the base metal what area do I use?
Av = t x b
t = Thickness of the base metal
b = Perimeter of the plug weld hole?
Thanks
I have a question regarding the plug weld design. Per AISC the base metal have to be checked per section J4. When I am checking the shear rupture for the base metal what area do I use?
Av = t x b
t = Thickness of the base metal
b = Perimeter of the plug weld hole?
Thanks