Point Reactions

[TTCorona132]

Hi all!

Apologies if this is in the wrong spot as I am new here.

This also may seem pretty basic problem, but there is some argument about it going on in my office so I wanted to see what others thought.

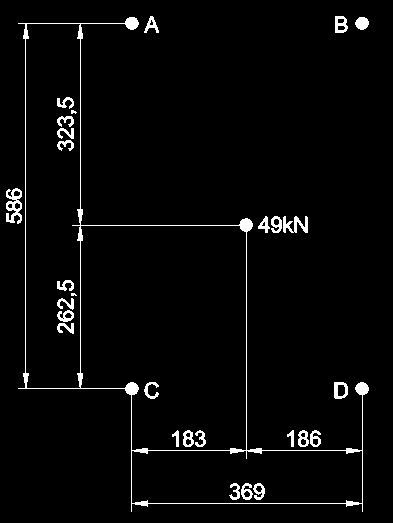
Below are two scenarios.
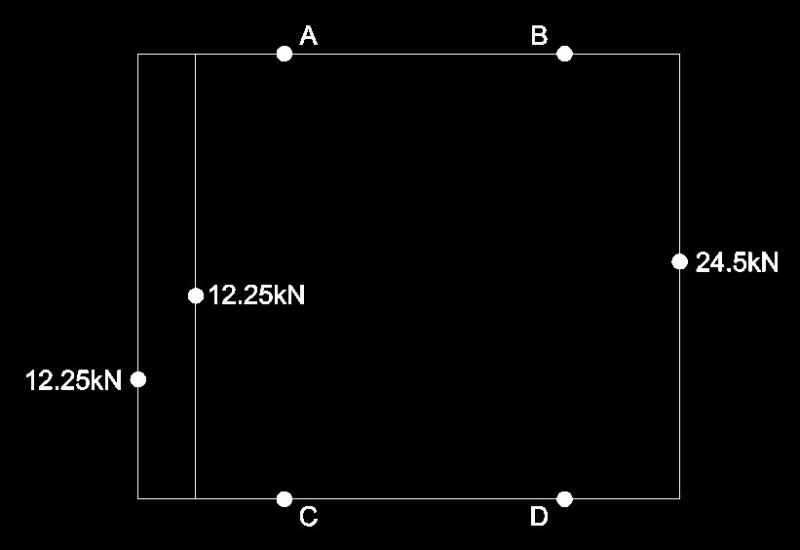
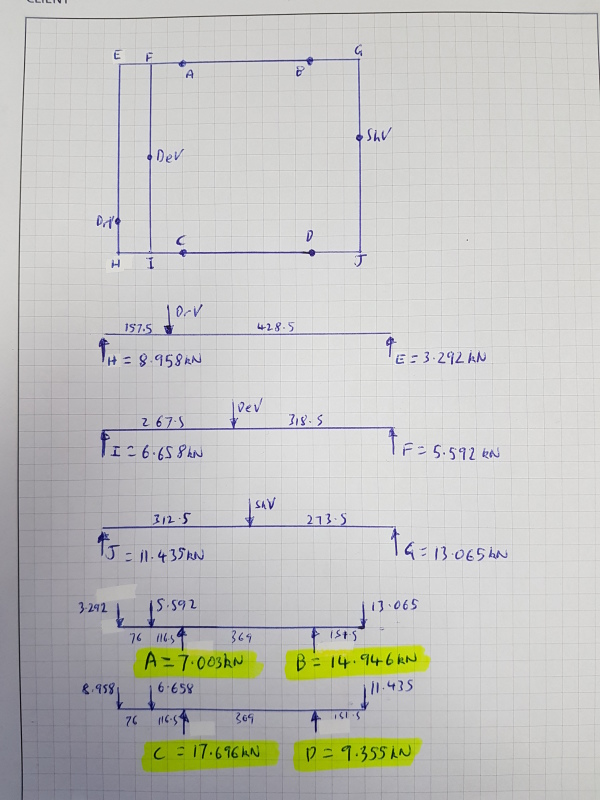
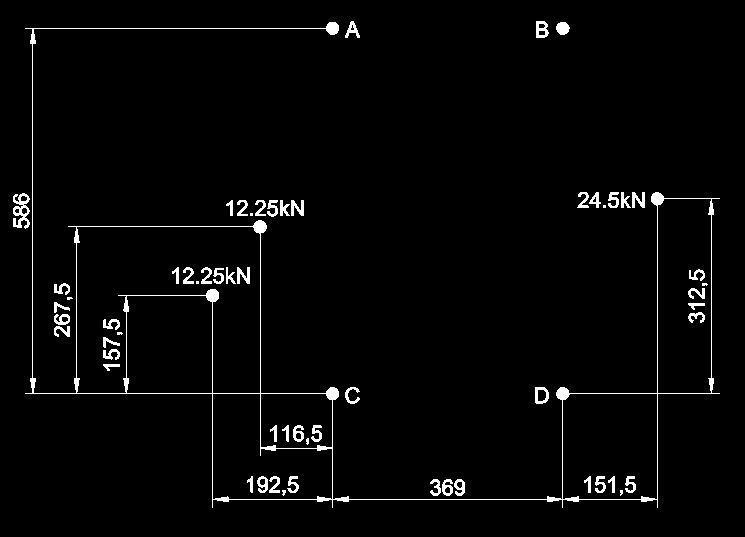
Basically just looking for the reactions at A, B, C and D
All loads shown are acting into the page.
The reaction points are rollers that can roll towards the AB end or the CD end

Look forward to you help
any tips pointers about the problems or the forum please let me know

Thanks
Mat

 

[TTCorona132]

Dimensions are in mm

 

[msquared48]

What is the structure here?

There is no information other than loads and dimensions. The structural layout is needed too.

Mike McCann, PE, SE (WA)

 

[ukbridge]

It depends on whatever actually constitutes the structure as Mike mentioned. Is it a slab, pilecap, something else?

I expect the answer you're looking for is what is the distribution of reactions under a point load load, P, at some x,y co-ordinate. This assumes a lot of things like:

1) Whatever provides the reactions are infinitely stiff, with no settlement
2) There is some kind of infinitely stiff structure connecting everything together like a slab.
3) The structure is statically determine i.e. one of the supports has a lateral and longitudinal restraint

Basically all you do is calculate the proportion of 'P' taken by rows AB and CD using simple statics/taking moments. This proportion of 'P' is then distributed to each reaction point A, B, C and D by taking moments in the opposite section. I'll do it for the 24.5kN point load:

Row AB = 24.5*312.5/586 = 13.0kN
Row CD = (24.5)(586-313)/586 = 11.4kN
Check AB + CD = 13.0 + 11.4 = 24.5kN, OK

For row CD say,

Push pull by inspection, RC = -11.4*152/369 = -4.7kN
RD = 11.4*(369+152)/369 = 16kN
Check RC + RD = 11.4kN, OK

 

[rb1957]

if you're only interested in the reactions at the four points, and if loading 2 is equivalent to loading 1 (looks like it) then I'd say the four reactions should be exactly the same for the two loadings.

another day in paradise, or is paradise one day closer ?

 

[JasonMcKee71]

That's easy. Tranform the forces to a vertical-to-screen force at the centroid of the rectangle and to a couple of moments about both horizontal and vertical (on-screen) axes. Then calculate the reaction assuming force and moments equilibrium.


Jason McKee
proud R&D Manager of
Cross Section Analysis & Design
Software for the structural design of cross sections
Moment Curvature Analysis
Interaction Diagrams
Reifnorcement Design etc.

 

[Archie264]

Aren't there four unknowns and three equations? What am I missing?

 

[rb1957]

yes, 4 unknowns three equations. but you can
a) assume the supports are equally stiff so each support reaction 1/4 the load plus/minus couples from the two offset moments,
b) use a least squares solution to over defined equations (which should give the same result).

i'd get 12.25 +- 49*1.5/(369*2) +- 49*30.5/(2*586)

another day in paradise, or is paradise one day closer ?

 

[TTCorona132]

Structure would look something like this

 

[Lomarandil]

That's not very clear either. Do you mean there are beams running in the AC direction that are supported by beams running in the AB/CD direction? Simple spans, or is there continuity not shown?

 

[TTCorona132]

The single load of 49kN is at the centroid of the three other load points

So for the single load.
Taking moments around an axis BD
AC=(49*186)/369 = 24.699kN

Taking moments around an axis AC
BD=(49*183)/369 = 24.301kN

A=AC*(262.5/586) = 11.064kN
B=BD*(262.5/586) = 10.886kN
C=AC*(323.5/586) = 13.635kN
D=BD*(323.5/586) = 13.415kN
Sum of Reactions = 49kN


Looking at the multiple forces individually

Force1
F1AC=(12.25*(369+192.5))/369 = 18.641kN
F1BD=-(12.25*192.5)/369 = -6.391kN

F1A=F1AC*(157.5/586) = 5.010kN
F1B=F1BD*(157.5/586) = -1.718kN
F1C=F1AC*(428.5/586) = 13.631kN
F1D=F1BD*(428.5/586) = -4.673kN

Other Forces worked out in the same way

F2AC = 16.118kN
F2BD = -3.868kN

F2A = 7.358kN
F2B = -1.766kN
F2C = 8.760kN
F2D = -2.102kN

F3AC = -10.059kN
F3BD = 34.559kN

F3A = -5.364kN
F3B = 18.430kN
F3C = 4.695kN
F3D = 16.129kN

Sum of individuals

A = 5.010+7.358-5.364 = 7.004kN
B = -1.718-1.766+18.430 = 14.946kN
C = 13.631+8.760-4.695 = 17.696kN
D = -4.673-2.102+16.129 = 9.354kN
Sum of reactions = 49kN

 

[rb1957]

having a "grillage" of beams, each statically determinate, greatly simplifies the problem.

another day in paradise, or is paradise one day closer ?

 

[TTCorona132]

Do you mean like this?

 

[ukbridge]

Quoting reactions and forces to 3 S.F...student or secondary steelwork designer you pick ; )

 

[TTCorona132]

haha sorry

at this stage just using the extra figures to make sure they match exactly
will pull them back in final calcs

 

[TTCorona132]

So that's two way's of working it out.
with both giving the same answers.

But others in the office believe that using the centroid load should give the same results for the reactions.
i.e as I calculated earlier.

AC=(49*186)/369 = 24.699kN
BD=(49*183)/369 = 24.301kN

A=AC*(262.5/586) = 11.064kN Compared to 7.00kN
B=BD*(262.5/586) = 10.886kN Compared to 14.94kN
C=AC*(323.5/586) = 13.635kN Compared to 17.70kN
D=BD*(323.5/586) = 13.415kN Compared to 9.36kN
Sum of Reactions = 49kN

 

[rb1957]

it was alluded to earlier ... there is a difference if there is a rigid black box joining the loads and their reactions or if there are discrete loadpaths.

but i'm smelling a bit of a rat ... both solutions give the same sum AC and BD (24.7 and 24.3), comparing your centroid solution with the earlier solution. and the same sums AB and CD.

also the "shape" of your centroid solution ... 12.25+1.385, +1.185, -1.185, -1.364
compares with 12.25+5.45, +2.69, -2.89, -5.25 ...
this says to me that the centroid solution is reacting way less bending ...
check the moments about the CG of the reactions for both sets of loads

another day in paradise, or is paradise one day closer ?

 

[TTCorona132]

So the load at the centroid position is attached to the individual load points via a steel wire rope.

Obviously this brings horizontal loads into the formula but for simplicity at this stage I was just working on the verticals as the horizontals should all cancel out.

So I guess my question is.. which is the best way to determine the correct reactions?

 

[wannabeSE]

TTCorona132,
Is this a plate or 5 beams or something else?

 

[TTCorona132]

The structure is as per this diagram

The load at the centroid in the attached to the individual load points via a wire rope

As I said.. It has been simplified at this stage to remove an horizontal loads, and just concentrate on the verticals.

So 49kN at the centroid
will equal 24.5kN on each side

so the two loads on the left hand side will both equally see 12.25kN
and the load on the right will see the 24.5kN load.

apologies if I am not being too clear...