post tension zone of influence

[structSU10]

I am investigating a PT garage that has some failed tendons throughout. I have been getting a handle on the amount of PT loss that is still acceptable to performance of the PT slabs on the basis of minimum effective post tensioning force to meet service and strength requirements. The one thing I am not sure on is how to determine the effective width where losing tendons becomes an issue locally.

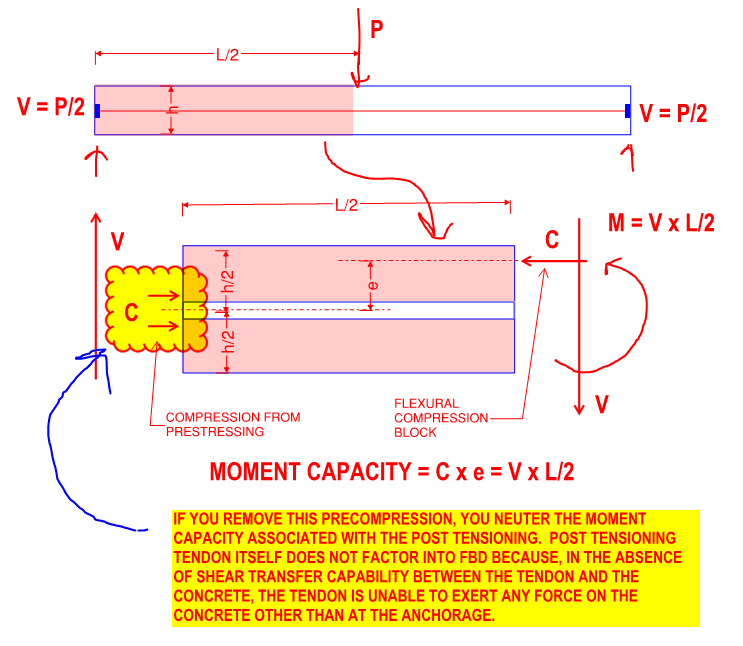
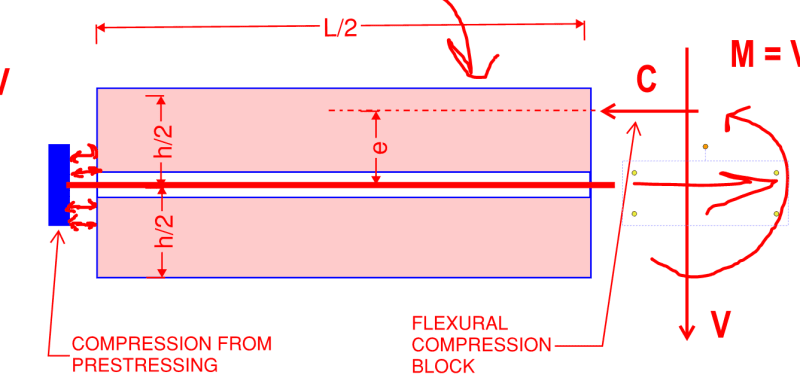
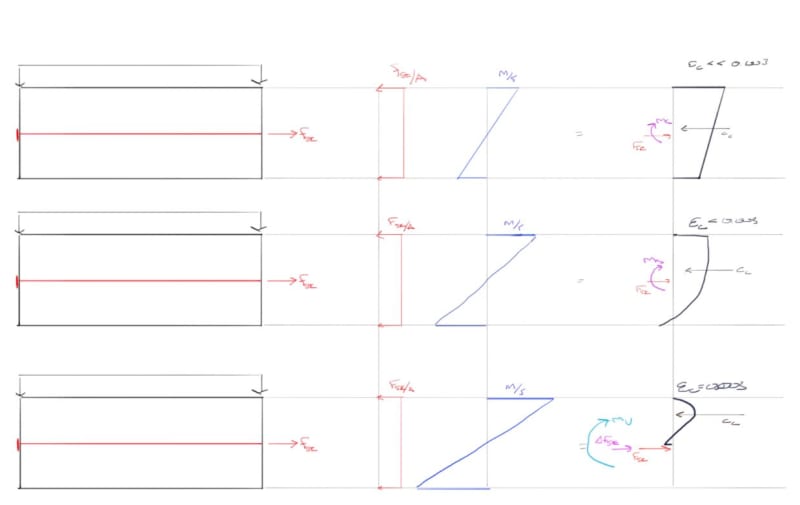
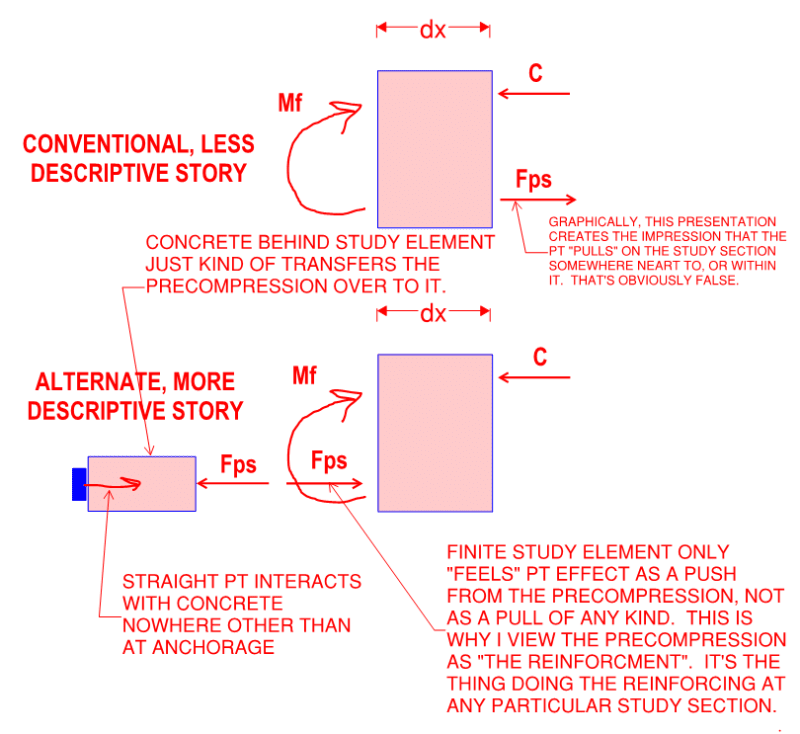
For example if the floor had 15 kip/ft effective post tensioning as designed and can safely perform with only 10 kip/ft, and tendons are spaced at about 2' on center and I have lost 3 tendons near each other but the remainder across a width are enough to provide the 10 kip/ft required, what is a reasonable criteria for a zone of a few tendons close to each other that may be broken? My thought is Poisson effect makes the overall compression spread pretty well across the width of the slab past a couple feet from the edge so perhaps the compression stresses can be assumed uniform but the reinforcement provided by PT is investigated locally? I could check a zone thats 4-6 times the slab span for the reinforcing present to check for adequacy. Does this sound like a reasonable approach or are there better methods?

 

[KootK]

1) Is this unbonded PT? I'll assume so.

My thought is Poisson effect makes the overall compression spread pretty well across the width of the slab past a couple feet from the edge so perhaps the compression stresses can be assumed uniform...

2) I agree that the discontinuity in compression probably does iron out pretty quickly. Maybe within the range of 1X-2X the gap between active strands.

3) For the compression to smooth out in this way it must travel laterally which raises the specter of a greater need for reinforcement parallel to the slab edge to restrain splitting. I wouldn't expect this to be a big deal for scenarios similar to the one that you've described however.

...but the reinforcement provided by PT is investigated locally?

4) In unbonded PT, the compression -- and not the strand itself -- IS the reinforcement. One way to think of it is that the curvature in the strands exert forces transverse to the slab (balancing forces) that shift the location of the compression vertically to be coincident with the strand. It's a mouthful, I know. Long story short: while a physical strand is a local thing, its "reinforcement" effect is still a fairly distributed thing, just like the compression.

5) If you lost a bunch of consecutives strands, your balancing forces would indeed be lessened in those areas. Again, though, for the kind of situation that you've been describing, I'd think that the slab's transvers flexural capacity would be capable of ironing this out laterally.

I could check a zone thats 4-6 times the slab span for the reinforcing present to check for adequacy. Does this sound like a reasonable approach or are there better methods?

6) Four to six times the slab span sounds optimistic to me. As you know, in the US, we use very wide design strips (often unpopular with engineers outside of north America). Checking your design strips in such a fashion is likely to yield favorable results. For this, I might revert to a column strip & middle strip type of analysis more like what is done in other parts of the world. That said, doing it the ACI way should produce a safe result from a ULS perspective. It just may do a poor job of capturing lateral stress distribution and, as a result, may not make serviceability issues apparent to you.

 

[structSU10]

Thanks for the feedback.

I have revised some of my thoughts as follows:

1. where I plan to use 16*t for an effective zone width (ACI T beam flange width)
2. I assume compression from the tendons is uniform past the first few feet on an 45 degree load spread of compression from the tendons per PTI tech note 1.
3. I establish a function that adjust balance / primary moment with reduced PT, and in turn adjust ultimate capacity of the section as well.
4. determine level of prestress loss / number of tendons that can be broken per 16*t width.

Regarding your point 4 - I still get to use As*fy of the PT in addition to the bonded reinforcement for the ultimate limit state though. I just use 1.2DL+1.6LL+1.0HYP wherein HYP take into account the 'reinforcement' from the PT to a certain extent, but the PT can be pushed a bit further for strength considerations.

I think near the anchorages, while the load is spreading out, there is potential for cracking due to a loss of the precompression - and perhaps a greater chance at general strength loss due to this effect - not sure how to bake that in right now.

 

[Ingenuity]

4) In unbonded PT, the compression -- and not the strand itself -- IS the reinforcement.

On such logic, a fully restrained unbonded PT slab (effectively no pre-compression) has no strength!

 

[KootK]

On such logic, a fully restrained unbonded PT slab (effectively no pre-compression) has no strength!

1) Not quite as you've still got the load balancing effect of the tendon drape. The end product sort of resembles a suspension bridge rather than a prestressed concrete member though.

2) Yes, having the pre-compression bleed off into restraining members does detract from the flexural capacity. And steps certainly ought to be taken to ameliorate that.

Do you really agree with my logic in #4 or is this just one of those "lets beat up on unbonded PT" things? I'm cool with either and just want to know where to focus my efforts.

 

[Ingenuity]

I disagree with your statement of: "In unbonded PT, the compression -- and not the strand itself -- IS the reinforcement."

To me, it brings up images that a externally compressed element with no internal reinforcement, and that is NOT the case.

Whilst I "beat up" on unbonded PT as a system, it also provides to me a significant source of income as I am forever repairing such systems - new 2021 ones too!

One way to think of it is that the curvature in the strands exert forces transverse to the slab...

How does you #4 logic work with a case of unbonded tendons placed mid-depth (no eccentricity) with no drape? You have no curvature effects until the member has deflected significantly, but the tendons are indeed 'reinforcement', even before they undergo 'curvature'.

To the OP:

Given only 15k/ft I assume you parking structure is a 1-way slab system, probably 5" to 6" thick (thin!!) slabs.

I just recently did an assessment to a 1-way PT slab, parking structure, tendons at 3' c/c. Slab is 7" thick. I initially started with 8 x slab thickness as a effective width, and had to extend that to about 10.2 times slab thickness (6') and justified ultimate strength on that basis. I did not check service stress (and there were no visible/excessive deflections) given that the condition is temporary (short-term), as the tendons will be repaired soon.

For 2-way slabs (most often banded-uniform design in North America) some forensic tech papers have reported 30% loss (or more) of PT before flexural capacities suffer:

As demonstrated in the case studies, modern two-way PT slab systems are surprisingly redundant and can require loss of 30 percent or more of the prestressing before flexural capacities drop below that required by code for new designs. This finding should provide the evaluating engineer with a useful frame of reference when evaluating a modern PT slab with distressed tendons.

 

[Settingsun]

Why doesn't the span factor into your effective width?

 

[Ingenuity]

Why doesn't the span factor into your effective width?

I adopted the effective width based upon max tendon spacing 'rules' (eg TR43 and AS3600 type requirements) that are independent of span.

Additionally, for my 1-way PT slab, there is no (zero) mild steel reinforcement to the slabs (top nor bottom). I had two unbonded T&S (no drape/distribution) tendons in the orthogonal direction that I used to calculate the transverse capacity of the slab to 'span' across corroded tendon/s. This structure was built in 1970 using 1/4" dia 240 ksi wire button-head tendons, wrapped in kraft-paper. A system with poor durability...and a royal pain in the 'you-know-what' to repair.

 

[KootK]

To me, it brings up images that a externally compressed element with no internal reinforcement, and that is NOT the case.

I disagree. If we simplify things by looking at an undraped, unbonded post tensioned member, I would say that is exactly the case. How could it not be since, in that scenario, all that the post tensioning does to the concrete member is exert a compression at the anchorages? Note that, for the purpose of this discussion, I'm assuming that there is no mild reinforcement in play.

How does you #4 logic work with a case of unbonded tendons placed mid-depth (no eccentricity) with no drape?

It works as shown in the equilibrium sketch shown below. Note that the sketch can easily be extended as follows:

1) Shifting the straight tendon provide to any vertical location does not appreciably change the model.

2) Introducing tendon curvature only modifies the effective, vertical location of the precompression.

 

[Ingenuity]

In unbonded PT, the compression -- and not the strand itself -- IS the reinforcement.

I am still confused (may be even bamboozled) by the above statement. Maybe it is just me!



1. We (or at least my understanding of what we are discussing) are talking about unbonded PT as 'reinforcement' as it applies to calculations for moment capacity i.e. ultimate strength, not service stresses.

2. An external compressed element without internal reinforcement (rebar nor PT) only compares to an internal prestressed element for concrete stress calculations (neglecting duct area etc), but not for ultimate flexural capacity.

3. You have drawn a FBD for a 'concrete-only' section, which is applicable for calculation of stresses on the concrete.

4. When you consider the FBD of the 'total-section' (with the tendon included) there will be a tension force, at mid-depth of the cut (for this example). This tension (tendon) force is NOT present in an externally pre-compressed element. Hence the difference.

 

[centondollar]

"1. We (or at least my understanding of what we are discussing) are talking about unbonded PT as 'reinforcement' as it applies to calculations for moment capacity i.e. ultimate strength, not service stresses."
Unbonded tendons provide low ductility in ULS (and low moment capacity if prestressing losses are large), since it is not connected to cross-sectional strain, unlike a bonded tendon. If a structure with unbonded tendons and no mild rebar, or very little mild rebar, is stressed to ULS, it will fracture in a brittle manner. Maybe this is why KootK was talking about serviceability as the relevant case for unbonded PT.


"3. You have drawn a FBD for a 'concrete-only' section, which is applicable for calculation of stresses on the concrete."
WIthout normal reinforcement, unbonded PT only provides SLS capacity. At ultimate limit state, with only unbonded tendons, there is negligible amounts of additional strain in the tendons (since their strain is not connected to the behavior of the cross-section) and thus negligible additional stress (<=100 MPa according to EC2) and thus negligible additional force and thus negligible additional moment capacity. Thus, in practice, mild reinforcement must be added for considerable ductility to exist in unbonded PT structures, and if the prestressing losses are large (i.e., unbonded tendon force at ULS is small), bending capacity is also much lower for unbonded tendons than for bonded tendons.


"4. When you consider the FBD of the 'total-section' (with the tendon included) there will be a tension force, at mid-depth of the cut (for this example). This tension (tendon) force is NOT present in an externally pre-compressed element. Hence the difference. "
For unbonded PT, the precompression is applied "externally", i.e. at the anchorages (anchorage block is pulled against concrete by tendons).

There is a tension force at the location of the unbonded tendon in this case - that is correct. However, the effect an unbonded tendon in ULS would be to provide force from initial strain & stress (after losses!) and a very small amount of additional strain (<=100MPa according to EC2), due to reasons explained above. Thus, KootK:s claim that "for unbonded PT, the compression is the reinforcement" is not incorrect per se.


EDIT: changed "WIthout normal reinforcement, unbonded PT only provides SLS capacity" to "Without normal reinforcement, unbonded PT provides limited ULS capacity (only the initial strain and stress from prestressing is used), and is thus usually not designed to withstand ULS loads without additional rebar".

 

[Settingsun]

3. You have drawn a FBD for a 'concrete-only' section, which is applicable for calculation of stresses on the concrete.

4. When you consider the FBD of the 'total-section' (with the tendon included) there will be a tension force, at mid-depth of the cut (for this example). This tension (tendon) force is NOT present in an externally pre-compressed element. Hence the difference.

I think if you do that, you only look at the section, not the length of beam back to the support. This shifta KootK's compression force at the anchorage to the tendon force at the section for the same resulr.

 

[KootK]

In unbonded PT, the compression -- and not the strand itself -- IS the reinforcement.

I am still confused (may be even bamboozled) by the above statement. Maybe it is just me!

I'm not surprised. The conventional presentation of flexural strength in unbonded PT does a poor job of elucidating this aspect of things in my opinion. It took me a long time to arrive at this particular insight and doing so required studying detailed FBD's of the concrete in isolation of the PT, treating all aspects of the post-tensioning as external actions.

The conventional presentation is obviously geared towards drawing parallels between PT design and ordinary reinforced concrete design in acknowledgement of the logical progression that most of us experience as designers. While expedient in that regard, I feel that presentation tends to obfuscate some important facets of unbonded PT mechanics.

1. We (or at least my understanding of what we are discussing) are talking about unbonded PT as 'reinforcement' as it applies to calculations for moment capacity i.e. ultimate strength, not service stresses.

That is my understanding as well. None of my previous comments were intended to speak to service level stresses. In the sketch that I posted previously, you will note that I depicted a cracked concrete section with a concrete compression block. It's decidedly ULS.

2. An external compressed element without internal reinforcement (rebar nor PT) only compares to an internal prestressed element for concrete stress calculations (neglecting duct area etc), but not for ultimate flexural capacity.

I disagree. Because unbonded PT is not composite with the concrete that surrounds it, I believe that PT can indeed be treated as an external action without any loss of rigor in the analysis.

3. You have drawn a FBD for a 'concrete-only' section, which is applicable for calculation of stresses on the concrete.

I contend that it is also applicable for a ULS flexural analysis. Again, this is made conveniently possible because the PT tendons are not composite with the concrete. At least not in the conventional sense of the word "composite" which is usually intended to imply the capacity for longitudinal shear transfer between the elements of the cross section.

When you consider the FBD of the 'total-section' (with the tendon included) there will be a tension force, at mid-depth of the cut (for this example). This tension (tendon) force is NOT present in an externally pre-compressed element. Hence the difference.

I see no difference. That tension force that you rightly described simply traverses the length of the member, without interacting with it, and expresses itself as s compression force delivered at the anchorage. And that is just as it would be with an externally pre-compressed element and how I showed it in my sketch which I've modified slightly below.

In a ULS event taken to the extreme, where caternary-ish stuff starts to develop, yeah, there's a difference. However, to my knowledge, we don't normally consider that in ULS flexural design calculations.

 

[KootK]

WIthout normal reinforcement, unbonded PT only provides SLS capacity.

I disagree strongly with that statement. I've never once seen a text book or standard that completely discounted unbonded PT's contribution to ULS flexural strength as you've suggested. And, certainly, that is consistent with my understanding of the fundamentals. I do agree that some bonded reinforcement should always be provided for ductility etc.

Thus, KootK:s claim that "for unbonded PT, the compression is the reinforcement" is not incorrect per se.

I appreciate your support, tepid as it may be. I'd prefer a little logical rearrangement though:

NOT INCORRECT = NOT ( NOT ( CORRECT ) = CORRECT = 100% CORRECT AND UNASSAILABLE

Yeah... that's better.

 

[Celt83]

In the hypothetical scenario where the entirety of the pre-compression was restrained resulting in no axial compression in the cross section from the unbonded tendon.

From table 20.3.2.4.1 in ACI 318-14:

Then fse is entirely reacted by the restraint so the only contribution to ultimate strength would be the 10,000+F'c/([100,300]p) component generated from the curvature change after stressing. Although if fully restrained against pre-compression you could probably argue the section is not post-tensioned and needs to be designed as mild reinforced neglecting the tendon entirely.

My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[Celt83]

this is how I look at it following loading from service through to ultimate.
If Fse was reacted by restraint then in the service cases Cc would need to be counteracted by concrete tension in the absence of other mild steel and at the ultimate limit state Cc would only be counteracted by delta Fse. ULS would also be reached much sooner.

My Personal Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

Open Source Structural GitHub Group:

https://github.com/open-struct-engineer

 

[KootK]

@Ingenuity: try this sketch on for size which, I think, echoes steveh49's comment. I'm not trying to be obtuse here but, rather, trying to find the particular way to present this that might get you onside with my perspective.

 

[centondollar]

"I disagree strongly with that statement. I've never once seen a text book or standard that completely discounted unbonded PT's contribution to ULS flexural strength as you've suggested. And, certainly, that is consistent with my understanding of the fundamentals. I do agree that some bonded reinforcement should always be provided for ductility etc."
I misspoke. I was referring to the fact that unbonded PT ULS has very limited ductility (force in tendons is at most "force after losses" + "<=100MPa" per code, and probably not much more in reality, due to the fact that unbonded tendons do not act compositely with the concrete), and that normal reinforcement is usually added to unbonded tendon systems for that reason.

If any and all design loads can be carried in SLS (as is commonly the case for unbonded tendon systems, i.e. anything but bridges), normal reinforcement can thus be kept to a minimum for unbonded tendon prestressed systems.

 

[KootK]

Then fse is entirely reacted by the restraint so the only contribution to ultimate strength would be the 10,000+F'c/([100,300]p) component generated from the curvature change after stressing.

That's an interesting perspective. The whole bleed off thing is, truly, the aspect of unbonded PT that I find most disconcerting. Consider:

1) You almost always have some bleed off so, in that respect, your flexural capacity is always overestimated.

2) The balancing load and precompression are complementary. If you bleed off your precompression, you'd think that you'd run the risk of exceeding your service cracking stresses generated by the balancing load pushing upwards (mid-span cracking at the top of your slab).

 

[KootK]

@centondollar: thanks for the clarification. I certainly agree with regard to the strain situation. Something related that we've discussed here in the past is how that effect tends to create a somewhat undesirable arching behavior in the concrete rather than true, flexural behavior. That, again, speaks to ductility concerns and informs our preference to have some bonded reinforcement in the mix.