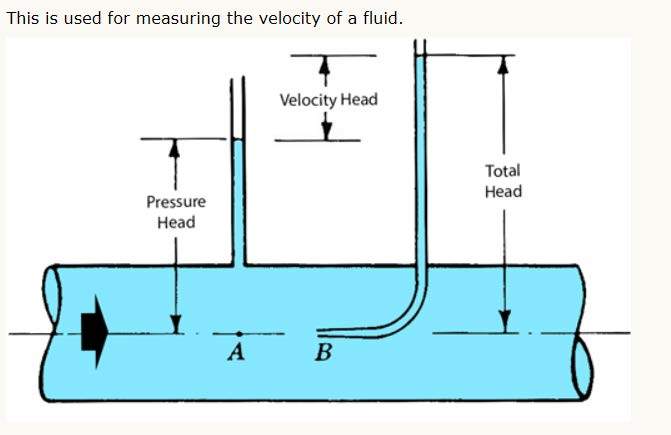
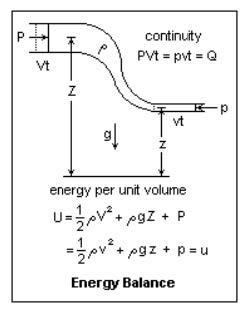
I've worked myself into a bit of a loop here.
A question came up from a younger colleague today that at first seemed a bit silly but after running a model I might see his point too. Basically, the question was if my pump discharge piping immediately sizes up say from 2" to 20" and I sized the line for pump discharge pressure, could I over pressure the line from almost all of my velocity energy being converted into static energy?
What's curious is that I ran a model with a 2" discharge, 3 inches long, into a 20" line for 10ft then back to a 2" into a tank. The software is telling me that my pump TDH is 40.38 feet, discharge pressure of 19.43 psig, in the 2" discharge piping I only have 4 psig of static head pressure. This seems to be telling me that a pressure gauge on this short section of discharge piping would only read 4 psig. The static pressure then jumps up to 19 psig in the 20" line. So it seems to be that discharge pressure gauges on pumps can be incredibly misleading in cases such as mine? That the TDH converted into pressure is total developed pressure also, but not necessarily static pressure or what I'll see at the discharge of the pump on a gauge? (Is this correct?)
Though converting the TDH into pressure still gives me the correct design data and I'm in no risk of over pressuring anything downstream, it does seem that my discharge pressure gauge readings need to be read in the context of my piping diameter, as my downstream pressure gauges could actually show an INCREASE in pressure if my diameter were to increase.
Am I understanding this correctly?
A question came up from a younger colleague today that at first seemed a bit silly but after running a model I might see his point too. Basically, the question was if my pump discharge piping immediately sizes up say from 2" to 20" and I sized the line for pump discharge pressure, could I over pressure the line from almost all of my velocity energy being converted into static energy?
What's curious is that I ran a model with a 2" discharge, 3 inches long, into a 20" line for 10ft then back to a 2" into a tank. The software is telling me that my pump TDH is 40.38 feet, discharge pressure of 19.43 psig, in the 2" discharge piping I only have 4 psig of static head pressure. This seems to be telling me that a pressure gauge on this short section of discharge piping would only read 4 psig. The static pressure then jumps up to 19 psig in the 20" line. So it seems to be that discharge pressure gauges on pumps can be incredibly misleading in cases such as mine? That the TDH converted into pressure is total developed pressure also, but not necessarily static pressure or what I'll see at the discharge of the pump on a gauge? (Is this correct?)
Though converting the TDH into pressure still gives me the correct design data and I'm in no risk of over pressuring anything downstream, it does seem that my discharge pressure gauge readings need to be read in the context of my piping diameter, as my downstream pressure gauges could actually show an INCREASE in pressure if my diameter were to increase.
Am I understanding this correctly?