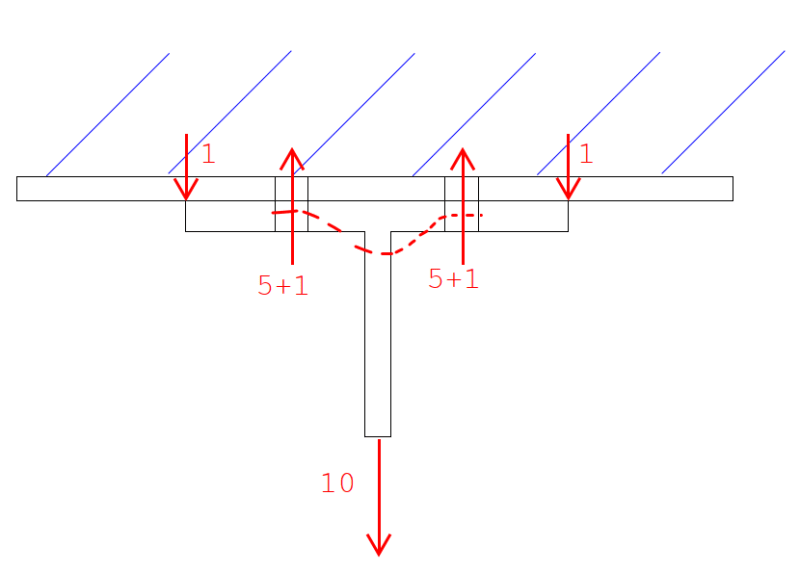
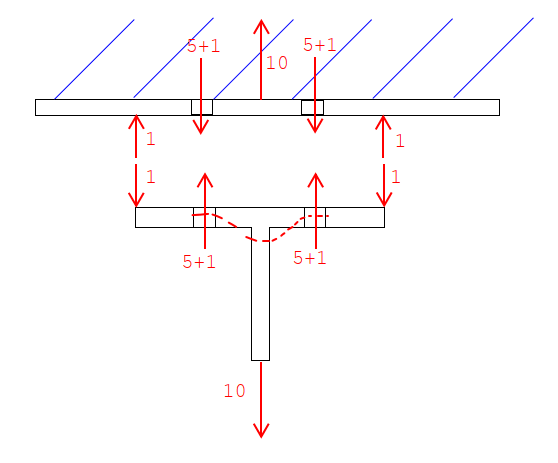
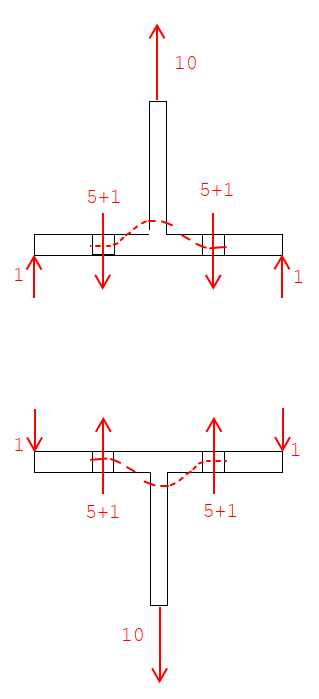
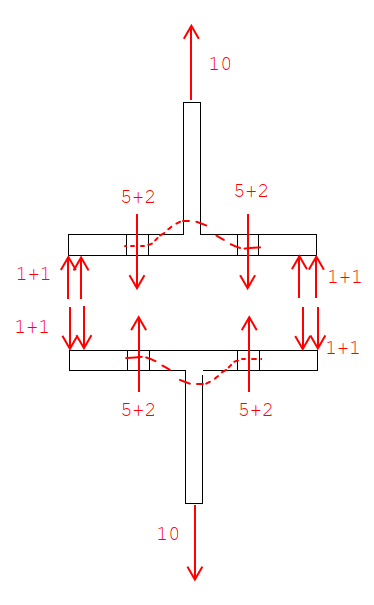
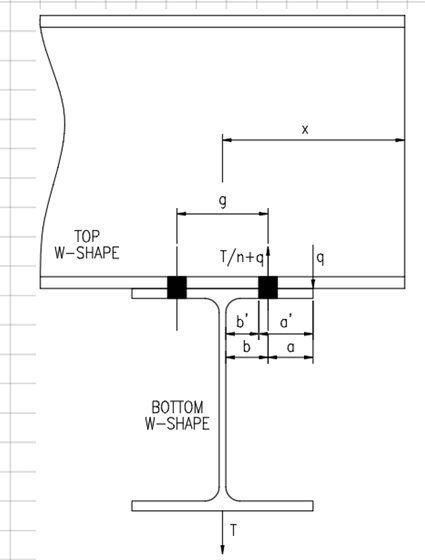
If both flanges would be considered flexible, would the upper flange not bend such that the two surfaces remain mated and therefore no prying occurs?
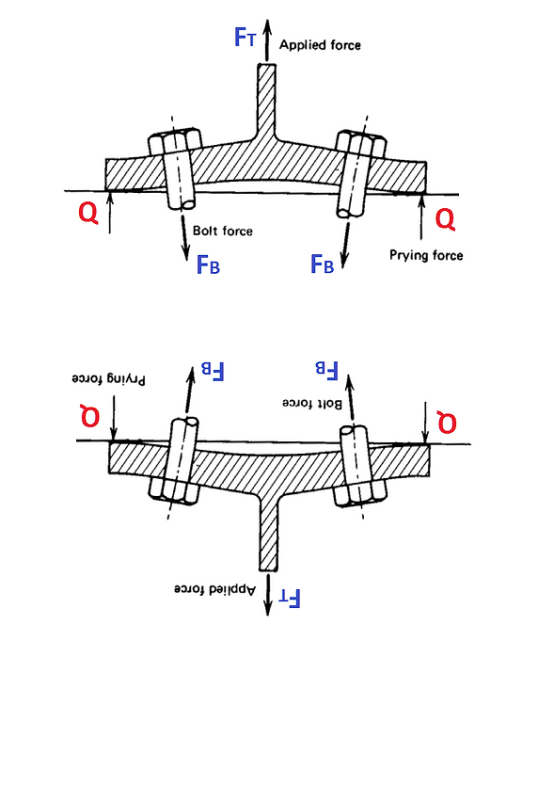
The tension in the bolts would pull down on the center part of the upper flange, and the resulting Q force would attempt to bend the upper flange outside of the bolts upward, forcing the upper flange to deflect in the same way as the lower flange, not in opposing ways. Maybe I'm missing something but in my head the two surfaces remain mated fully. At a minimum, due to this flexibility of the upper flange, I wouldn't think they're additive as there is only one force creating the entire scenario. Similar to a tension tie between two moment frame column bases. You don't add the two reactions, one cancels the other out.
Edit: perhaps I've figured out why my scenario wouldn't happen, the orthogonal orientations would have the webs acting as stiffeners preventing the mating I was describing. If there were stiffeners added in the other directions to both the upper and lower beams, does the prying become eliminated as now you'd have two stiff plates connected to each other?


![[tiphat] [tiphat] [tiphat]](/data/assets/smilies/tiphat.gif)