stressebookllc
Aerospace
Dear Friends, I have a bracket, a simple L bracket, with a couple of fasteners holding it down at the bottom base leg, and a horizontal pull away load at the top leg.
I am trying to figure out the reactions with hand calculations.
Two other scenarios are fairly straight forward statically determinate problems where the load is either pulling the top leg up or pushing it towards the fasteners and so are the hand calcs.
I have a couple of videos explaining them if you want to check them out:
But the Pull away load scenario is a statically indeterminate problem with more unknowns than known equil. equations.
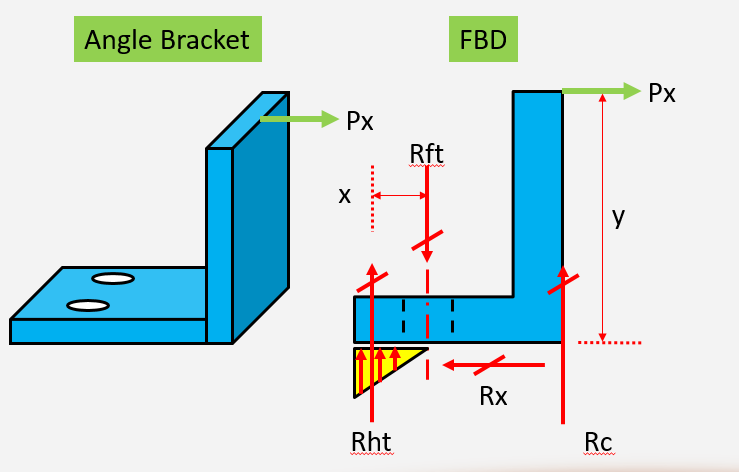
See figure below:
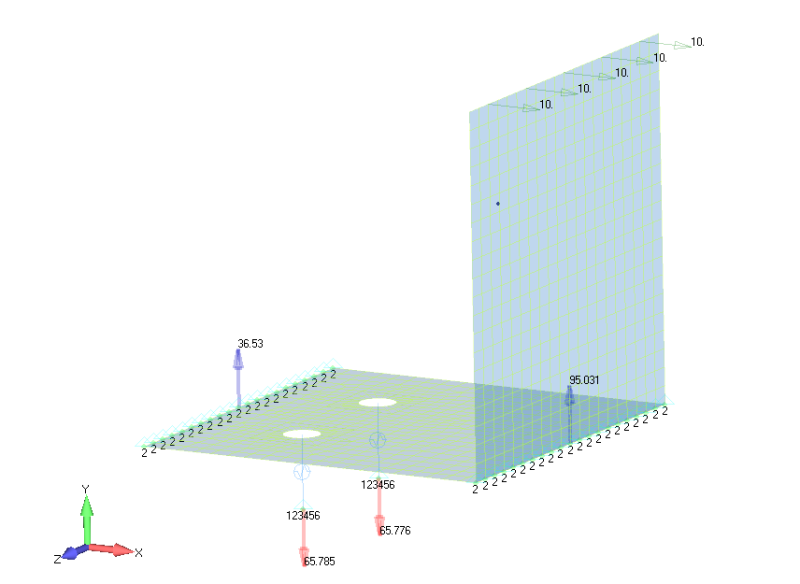
I built an FEM with the bottom L corner and the edge of the bottom leg constrained along Y (vertical) and the fasteners constrained along XYZ. You can see the running load of 10lb/in.
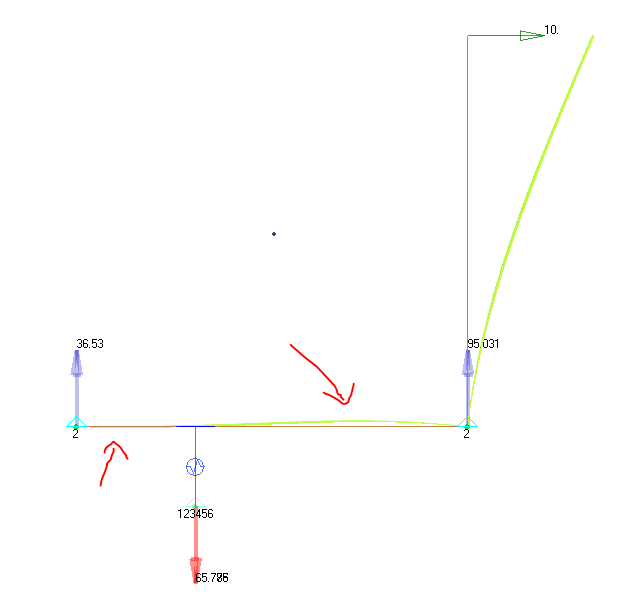
The reactions are as follows (don't worry about the long CBUSHs at the fasteners, and also I am only showing Y FBD loads, also assume the heel toe from the FBD above is not there, shift it to the edge)
So is there any way we can calculate these using hand calculations? Its an approximately 5"x5"x5" angle and fasteners are at 3.4375" from corner. You don't ned to use exact dimensions.
Which law of compatibility can be used here to get that third equation I need to solve for all three reactions?
Also list your equilibrium equations please.
Thanks.
Aerospace Stress Analysis and FEA Courses
Stressing Stresslessly!
I am trying to figure out the reactions with hand calculations.
Two other scenarios are fairly straight forward statically determinate problems where the load is either pulling the top leg up or pushing it towards the fasteners and so are the hand calcs.
I have a couple of videos explaining them if you want to check them out:
But the Pull away load scenario is a statically indeterminate problem with more unknowns than known equil. equations.
See figure below:

I built an FEM with the bottom L corner and the edge of the bottom leg constrained along Y (vertical) and the fasteners constrained along XYZ. You can see the running load of 10lb/in.
The reactions are as follows (don't worry about the long CBUSHs at the fasteners, and also I am only showing Y FBD loads, also assume the heel toe from the FBD above is not there, shift it to the edge)

So is there any way we can calculate these using hand calculations? Its an approximately 5"x5"x5" angle and fasteners are at 3.4375" from corner. You don't ned to use exact dimensions.
Which law of compatibility can be used here to get that third equation I need to solve for all three reactions?
Also list your equilibrium equations please.
Thanks.
Aerospace Stress Analysis and FEA Courses
Stressing Stresslessly!