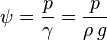Pump Pressure and Head

[DJB82]

The energy provided by a pump is measured in terms of head. This is independent of the liquid density. How would you prove this from a mathematical point of view. The formula for static head has a density term in it. So then how could head not be related to density. Any help clarifying this would be appreciated.

 

[georgeverghese]

Energy provided by the pump is measured by flow and head and pumping density and pumping efficiency:


Watts = Q x rho x g x h / E

Q = m3/sec
rho = kg/m3
g = 9.81 m/sec2
h = head produced at Q
E= efficiency (as a ratio, not %)

This W is plain absorbed power - there are other adders to account for seal losses, gearboxes and couplings, etc.

Yes, in a centrifugal pump, the head developed is independant of density, but there may be some corrections required for viscous fluids when internal slippage becomes significant. This comment refers to newtonian fluids only.

 

[desertfox]

Hi

Read this link it may help:-

http://www.pumpfundamentals.com/yahoo/The influence of specific gravity on total head.pdf

 

[LittleInch]

DJ882,

As the other above say, you have mistaken the head figure for energy. Head is head (m), not energy. Only once something starts moving then the density term comes into play.

Head from a centrifugal pump is a function of impellor diameter, impellor shape and rotational speed. It generates a velocity which translates into head - a distance. Distance cannot be energy.

If the pump is not flowing and the outlet is blocked, there is still head / pressure, but no energy in the fluid.

When I first started looking at pump design and operation it took me some time to get my head around the head concept, but when you do, it all starts to make sense.

Remember - More details = better answers
Also: If you get a response it's polite to respond to it.

 

[EmmanuelTop]

The first two sentences in your OP are contradictory to each other:

The energy provided by a pump is measured in terms of head.
This is independent of the liquid density.

Energy supplied to the fluid is very much dependent on the fluid density. You can observe this easily by measuring and comparing motor amps in cases when you pump the same amount of gasoline (d=0.75) and water (d=1.0).

Lifting 1 cubic meter of feathers does not require the same energy as lifting one cube of steel. E=m*g*dH
H is the same in both cases, but the energy is not.

Dejan IVANOVIC
Process Engineer, MSChE

 

[bimr]

In fluid mechanics, pressure head is the internal energy of a fluid due to the pressure exerted on its container. It may also be called static pressure head or simply static head (but not static head pressure).

 

[BigInch]

Look at it from a KINETIC ENERGY perspective.

KE = 1/2 * m * v^2
with mass = 1 lbm, then KE = 1/2 * v^2

KE also = m * g * h, when in a gravitational field and h = height above datum

mgh = 1/2 m v^2, which for a mass of 1 lbm
where h is "head".
head therefore = v^2 / 2 / g

Kinetic Energy is not independent of mass.
Head is independent of mass, because Head is defined as the kinetic energy PER UNIT MASS.

 

[BigInch]

Correction
PE in a gravitational field = mgh

 

[DJB82]

Thank you everyone for taking the time to respond, much appreciated. I've been reviewing your comments and doing a lot of reading on the different types of head (static,dynamic, elevation)in relation to pumps, so as to develop my knowledge. I was wondering if anyone could help me again with the following;

If I wanted to gdetermine the flowrate directly at the outlet of a centrifugal pump that is in operation, I could do the following:
(For the purposes of this first scenario lets assume that I have a pressure gauge (bourdon mechanical) at the pump inlet and outlet and I know the fluid velocities at both the pump inlet and outlet).
- Convert the gauge readings to static head and add the relevant dynamic head terms to the inlet and outlet static heads (I believe that the gauge doesn't account for dynamic head if the liquid is flowing?). Then subtract the calculated suction head from the discharge head to determine the pump differential head. Then I can read the flowrate from the pump curve.

If I wanted to determine the pump shut off head I could
- Close a valve on the outlet of the pump that is downstream from the pressure gauge (the idea being to reduce the velocity to 0, so that any velocity head (dynamic) terms on the suction or discharge side of the pump become zero due to zero flowrate). Then use the gauge readings to work out the suction static head and discharge static head. Then subtract inlet from outlet which would give me the shut off head for the pump.

I don't know how right or wrong I am with the above approaches but would appreciate any comments.

 

[BigInch]

No. Flowrate in a pump is based on the size. Pumps of different sizes can have vastly different flowrates at similar inlet and outlet pressures, provided that they have sufficient power to do so.

 

[desertfox]

Hi DJB82

If you have the velocity of the fluid at the pump outlet then if you just multiply that by the area of the outlet you will obtain the volumetric flow rate.

 

[DJB82]

Thanks for taking time to reply.

I understand that different pumps can give much different flowrates even though the pressures may be similar. However if the pressures are similar and if the head is also similar then is this not where the pump curve for the specific pump in question comes into play?. The pressures/head may be similar for 2 totally different size pumps but when the pump curve is referenced then a similar head for 2 different pumps can yield a totally different flowrate depending on the curve that is specific to the pump in question.

In most situations that I encounter the only thing I have to reference is a pressure gauge/s near the pump and a pump curve (Head v flowrate). So if my above thinking is not correct then how would I use the pressure gauges to ultimately work out the flowrate (assuming I don't know any velocities at the pump inlet flange or outlet).

 

[BigInch]

You didn't say that you had a pump curve to help you. I thought you just wanted to guess a flow rate based on the diff pressure alone.

So in that case, yes you can estimate the flow rate based on the differential pressure converted to head. It might get tricky on a flat part of the curve.