sticksandtriangles
Structural
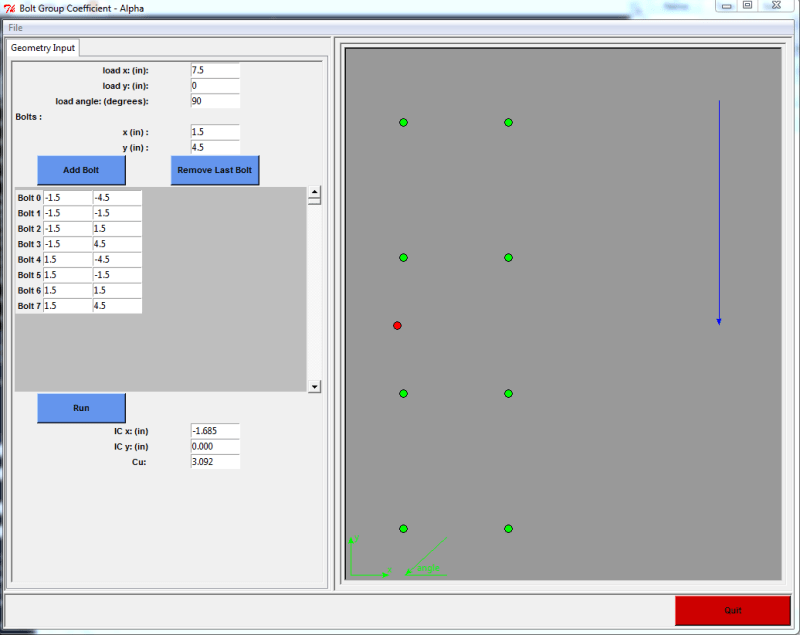
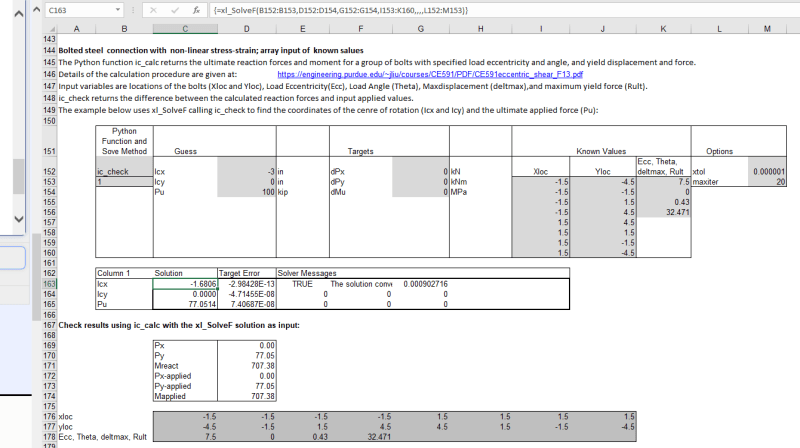
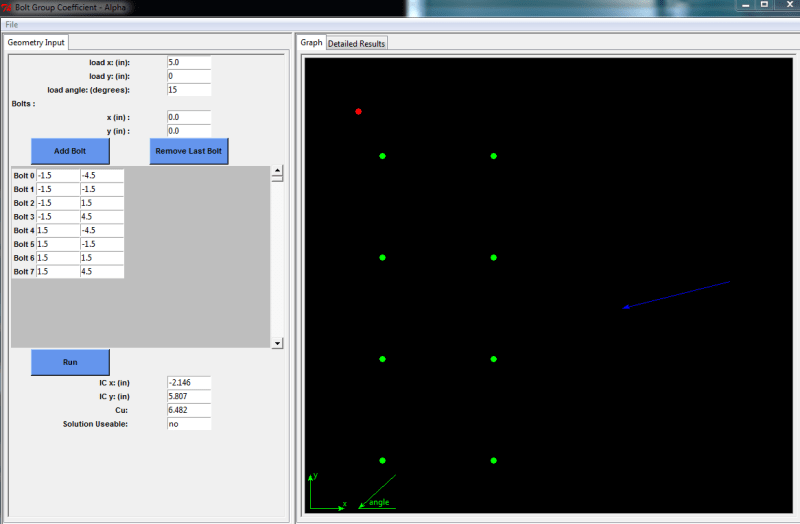
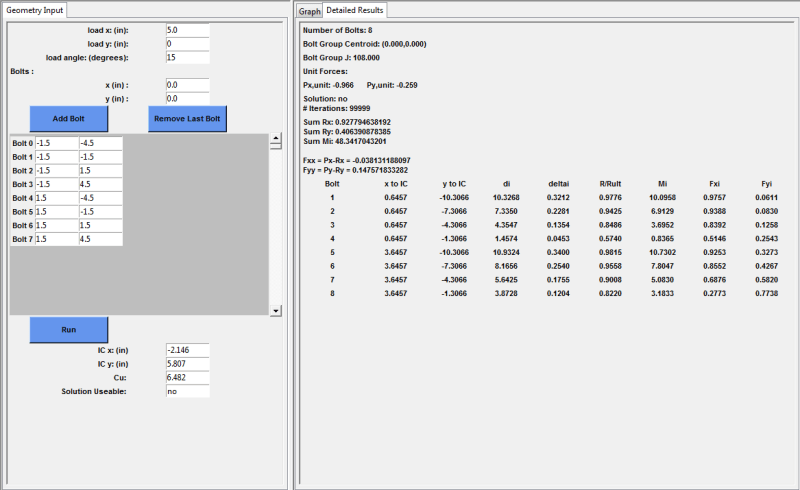
sparked by the python coding discussion by Celt83, I am diving in and trying to solve instantaneous center of rotation problems with python.
The example problem I am trying to solve is outlined here:
The way I see this problem, there are (3) unknowns:
[ol 1]
[li]X location of the instantaneous center of rotation, [/li]
[/ol]
[ol 2]
[li]Y location of the instantaneous [/li]
[/ol]
[ol 3]
[li]and the Applied Loading that needs to be maxed out.[/li]
[/ol]
(sorry don't know how to fix the numbering above, fiddled for too damn long)
I also have (3) equations that need to equal 0
[ul]
[li]Sum of Forces in the X = 0[/li]
[/ul]
[ul]
[li] Sum of Forces in the Y = 0[/li]
[/ul]
[ul]
[li]Sum of Moments = 0 [/li]
[/ul]
Even in my "native coding language" matlab, this would be somewhat challenging to code, so I am sure it will be fun using this as a learning experience in python.
Anyways, python experts, do you have any suggestions on how to solve this? Should I explore symbolic notation within in python? Should I use a solve block that iterates through the (3) unknowns?
Any help or suggestions/starting points would be appreciated.
My base code that does the guess and check version of this is shown below:
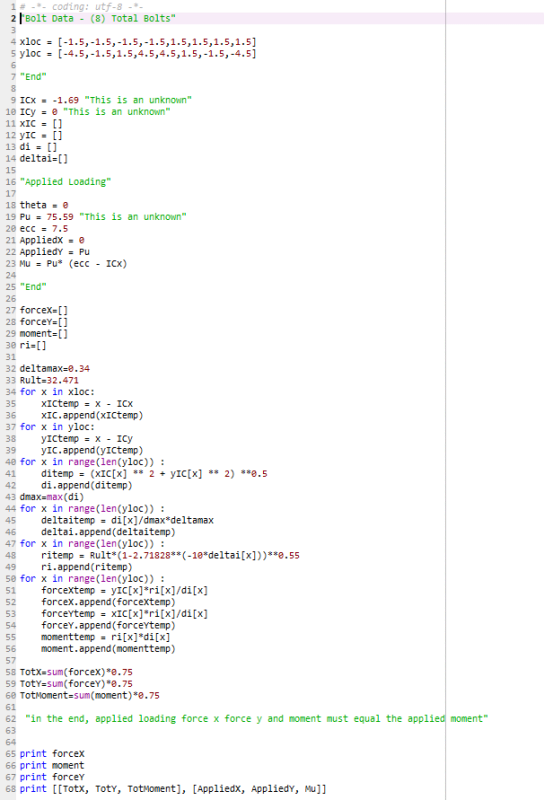
The final print shows the comparison of applied loading verse resist force.
S&T
The example problem I am trying to solve is outlined here:
The way I see this problem, there are (3) unknowns:
[ol 1]
[li]X location of the instantaneous center of rotation, [/li]
[/ol]
[ol 2]
[li]Y location of the instantaneous [/li]
[/ol]
[ol 3]
[li]and the Applied Loading that needs to be maxed out.[/li]
[/ol]
(sorry don't know how to fix the numbering above, fiddled for too damn long)
I also have (3) equations that need to equal 0
[ul]
[li]Sum of Forces in the X = 0[/li]
[/ul]
[ul]
[li] Sum of Forces in the Y = 0[/li]
[/ul]
[ul]
[li]Sum of Moments = 0 [/li]
[/ul]
Even in my "native coding language" matlab, this would be somewhat challenging to code, so I am sure it will be fun using this as a learning experience in python.
Anyways, python experts, do you have any suggestions on how to solve this? Should I explore symbolic notation within in python? Should I use a solve block that iterates through the (3) unknowns?
Any help or suggestions/starting points would be appreciated.
My base code that does the guess and check version of this is shown below:

The final print shows the comparison of applied loading verse resist force.
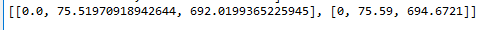
S&T

![[spin2] [spin2] [spin2]](/data/assets/smilies/spin2.gif) , lots of learning to ensue...
, lots of learning to ensue...