Question about Idelchik's Diag 4.10 resistance problem (Error in Aij from my end?) 1

[pumpkinwiz1]

Hello, I am trying to solve the laminar sudden contraction case as described in Idelchik's textbook.

For some reason, I am getting a very large negative value for the coefficient.
I have the following variables defined:
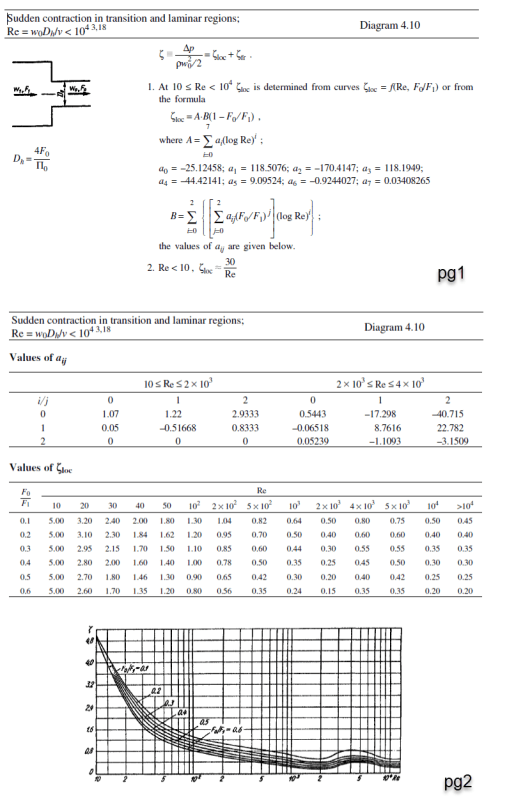
Re=1961
F0=1.45e-4 (meters[sup]2[/sup])
F1=.0018 (meters[sup]2[/sup])
I am ignoring coefficient due to friction for this case.

I am getting A= -2833 and B=1.2893, which gives the coefficient of -3300, which is wrong.
According to the graph in the textbook, it should give me a coefficient value of ~0.5

I think I might be doing something wrong in the summation:
When there is a sigma sum of aij indices as shown, I was assuming both A and B should result in a scalar value? I think I might be wrong because the equation to solve for the overall coefficient asks for A dot B(1-f0/f1).

Will appreciate any advice/feedback. Thank you!

 

[shvet]

My calculation of A gives

lgRe = 3.3
0 = -25
1 = 390
2 = -1847
3 = 4219
4 = -5218
5 = 3521
6 = -1172
7 = 143
Total = 10.5

I did not check B

Be ready that Idelchik contains a lot of misprints, e.g. the copy I have states

 

[pumpkinwiz1]

Hello, thanks for the reply! Turns out in my script and calculation I had to use log10 (Ln) instead of normal log. I am getting the answers aligning with the text now.

One side note- I did notice there were a lot of erratas for Idelchik's textbook. my screenshot is from the 4th edition.

I cannot interpret the Russian writing in your screenshot- but the text in the version I copied does include the description that it is for transition & laminar regions, and therefore I think the version I see in yours might be a misprint (which is quite substantial in my opinion and hoped that was corrected)