Question regarding Ultimate Limit State Design 12

[fracture_point]

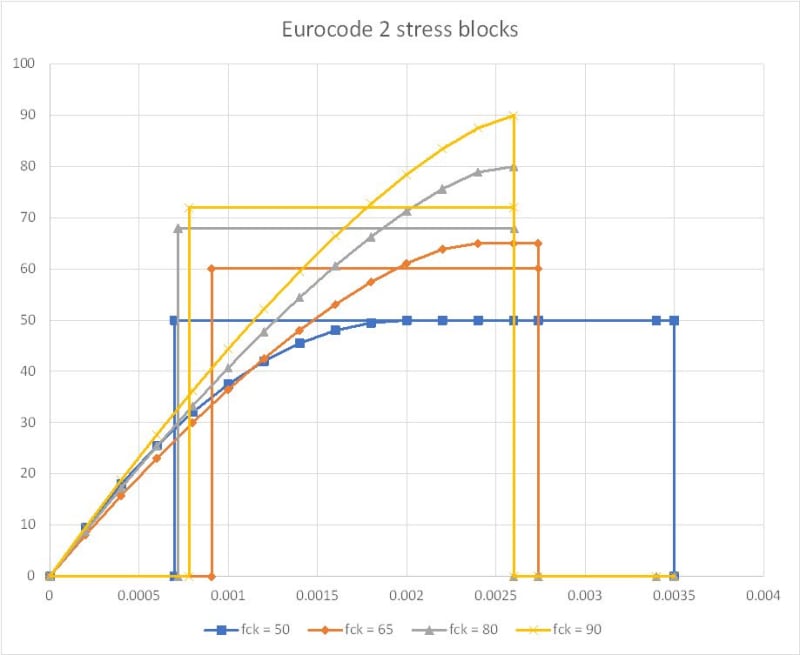
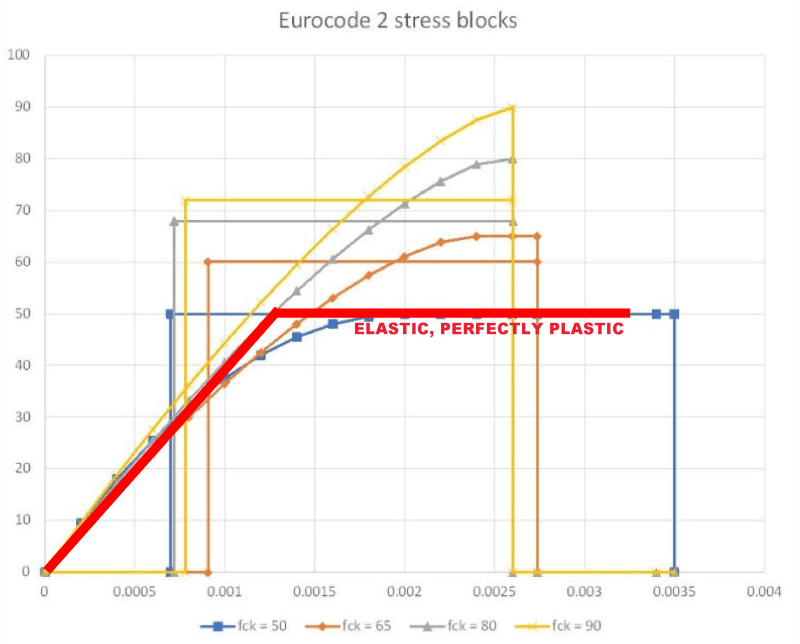
I was doing some additional background reading on ULS design, and found the following quote on wikipedia:

The ULS condition is computationally checked at a certain point along the behavior function of the structural scheme, located at the upper part of its elastic zone at approximately 15% lower than the elastic limit. That means that the ULS is a purely elastic condition, located on the behavior function far below the real Ultimate point, which is located deep within the plastic zone.

I can't find a reference for the approximation of 15%. We perform sectional analysis of members based on the plastic condition, and these loads are based on partial factors of safety to materials and loads. But I can't find anywhere that provides details about it remaining elastic.

 

[r13]

Blackstar,

You brought up a very interesting question on the "plastic capacity". Now let's go one step further, op top of Mp, sometimes we will have axial load too. Assume superposition is valid, what is the result when a hinged location subjects to both Mp+T, or C, simultaneously? May this phenomenon will never occur, or there is a simple explanation? Maybe you, or someone can help me to get over it.

 

[r13]

dik,

Be prepared, it is an hour long video, coffee break excluded But it's quite valuable in knowing how to squeeze a few drops out from the code to add some extra strength for the design. Enjoy it.

 

[dik]

I'm about half way through it... it's a great discussion on probabilistic design...

Dik

 

[Tomfh]

The current code specified structural resistance capacity calculations are well remain in the elastic range, thus the use of Fy in the equations

The use of Fy does not imply the elastic range.

If you use plastic section modulus (eg Blackstars diagram) you are assuming the section has gone past the pure elastic zone, and is sufficiently plastically deformed that the entire section is now yielding, is now plastic. Hence “plastic section modulus”.

 

[rapt]

Codes limit the stress at ultimate to the yield stress. That does not mean the section does not go into the plastic range. Just that you cannot benefit from the increased steel stress. Unless a designer does a Balanced Design (concrete strain of .003 - .0035 and steel strain of .002 - .0025), the strain in the steel will be greater than the yield strain, so the section will be in the plastic range. Very few designs are Balanced Sections. A design with minimum tension reinforcement would normally have a steel strain at ultimate in the order of .04 to .05 while the yield strain is .002 - .0025 (that is why low ductility reinforcement is a problem!).

The important thing is for the section not to go into the plastic range under service loads. Some codes specifically do not allow this. AS3600 and Eurocode specifically limit the steel stress at service to 80% of the yield stress. In most situations, this will be controlled automatically by the load factors at ultimate compared to service and the material/capacity factors at ultimate. With those set to normal design values, the steel stress at service would normally be in the range of 60-65% of the yield stress.

 

[r13]

Just find this.

k = M_p/M_y = Z/S
k = 1.5 for rectangle shape, and k ≅ 1.1 for I (W) beam
So, for steel wide flange shape, Z ≅ 1.1*S
LRFD Moment Capacity ∅Mn = = 0.9 M_p= 0.9*Fy*Z = 0.9*Fy*1.1*S = 0.99*FY ≥ Mu

Someone may want to try other shape.

 

[IDS]

In your blog, I am confused with the statement below, can you clarify? Thanks.

The two BS codes are limited to a concrete cube strength of 65 MPa, which is equivalent to a cube strength of a little over 50 MPa. The other codes have modifications to the concrete stress block for higher strength grades, to account for its reduced ductility.

Eurocode2 allows ULS design using a parabolic-linear stress block, or a rectangular stress block that will generate approximately the same force and moment (on a rectangular section). They also have a triangular-linear stress block, but this is just a conservative simplification of the parabolic-linear case.

As the concrete strength increases from 50 MPa to 90 MPa:
- The maximum strain reduces from 0.0035 to 0.0026
- The strain at the start of the constant stress region increases from 0.002 to 0.0026
- The exponent of the "parabolic" region reduces from 2 to 1.4
- The depth and maximum stress of the rectangular stress block is factored to be equivalent to the modified parabolic-linear stress block

See graph below.

The Australian code does not have any provisions for a parabolic-rectangular stress block, but it does modify the rectangular stress block factors to have a similar end result.




Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[dik]

Or the one I've been using for the last 50 years... I was introduced to it in 1st year engineering by the late Al Lansdowne, who would become my thesis adviser.

Dik

 

[IDS]

k = Mp/My = Z/S
k = 1.5 for rectangle shape, and k ≅ 1.1 for I (W) beam
So, for steel wide flange shape, Z ≅ 1.1*S
LRFD Moment Capacity ∅Mn = = 0.9 Mp= 0.9*Fy*Z = 0.9*Fy*1.1*S = 0.99*FY ≥ Mu

There is no dispute that in most cases if a load equal to the factored down design capacity is applied to a section then, the stresses will be less than the yield stress. The point is that this requires that the load does not exceed the design load, the load is distributed as assumed in the design analysis, and the section is constructed exactly in accordance with the design, with materials that meet or exceed the design assumptions, and with no degradation over time. If all that is true, the section is not approaching the Ultimate Limit State. The whole point of the ULS check is to allow for cases where some or all of those assumptions are not met.

It's not just seismic loads that may cause problems. For instance differential settlement, corrosion, or another section on the load path being stiffer or less stiff than assumed can all cause significant overstress, even with loads within the design limits.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[IDS]

Or the one I've been using for the last 50 years... I was introduced to it in 1st year engineering by the late Al Lansdowne, who would become my thesis adviser.

As mentioned, the Eurocode also includes a triangular-linear stress block.

Rather strangely, the way it is implemented makes it not only more conservative than the parabolic-linear stress block (which is reasonable), it is also more conservative than the rectangular stress block. For a given depth of neutral axis, both the force and moment are reduced.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[rapt]

Eurocode clause 3.2.7 also allows a designer to take into account strain hardening as long as the reinforcing strain is limited.

 

[dik]

IDS:
"Rather strangely, the way it is implemented makes it not only more conservative"

I still feel comfortable with my 'over design'... and have been using plastic design for nearly 50 years. I have little use for the increased UTS above yield since deflection usually 'kicks in'. Thanks for the added info, though. I wasn't aware other codes make allowance for the stain hardening.

The only thing this thread is missing is the inclusion of Luders bands and body centered cubic lattices...

Dik

 

[IDS]

dik - it was just the Eurocode formulation that I was saying was more conservative. It all depends where you take the end of the elastic strain, and what you use for the constant stress. For a rectangular section it's quite easy to work out numbers for a rectangular block that will give exactly the same results as the parabolic-rectangular block. For a non-rectangular section, or rectangular under bi-axial bending, the parabolic-rectangular gives much better results than the rectangular though, and the triangular-rectangular would be very close.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[dik]

Thanks, Doug... I'm just a tekkie junkie.

Dik