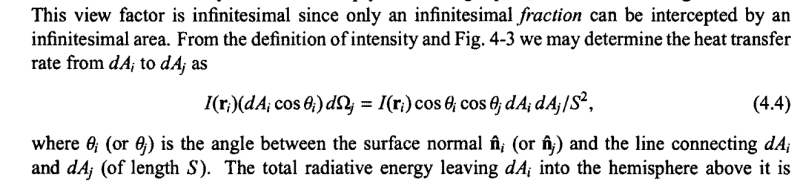gahhhrrrlic
Mechanical
- Jan 3, 2022
- 4
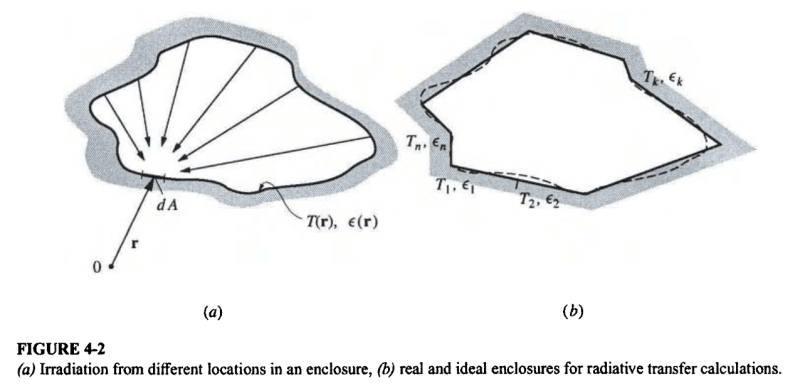
So I have consulted multiple sources both in books and online regarding the various view factor geometries and their formulae but I've yet to find one where the outer shell of a hemisphere (convex surface facing up) is situated in the center of a square cavity and exposed to the inside surfaces of that cavity. Is there a formula for that? I would think if you have a hemisphere in the middle of a box, the view factor would be a little more than 50% because some parts of the hemisphere would "see" more than half the box over its horizon but this is just an intuitive guess. I can't find the formula anywhere. Any help would be much appreciated. Thank you!