Hello, everyone!
I worked closely with the OP (cirokos) on this simulation. I read all the posts here and I wanted to add some information to let everyone know what we've tried, in the hope this might be useful to someone else in the future.
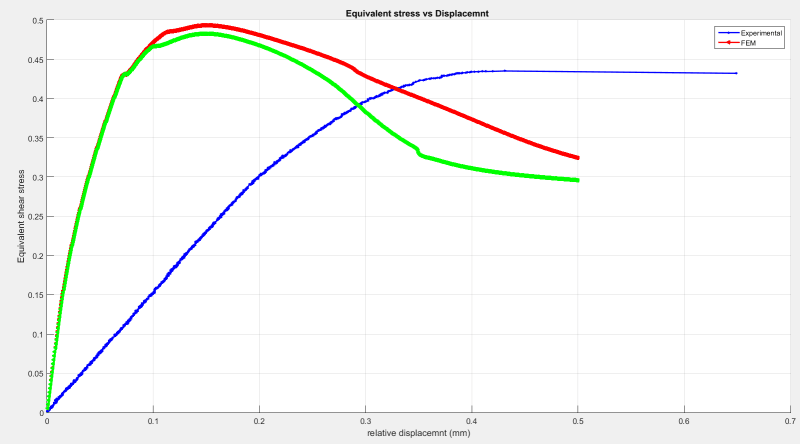
At first, when the OP came to me with the mismatching plots, I thought there was some major thing wrong with this simulation, like many of you suspected (wrong BC's, etc.). But this is a very straightforward model, and as I investigated in-depth I couldn't find any obvious errors.
We were left with less obvious alternatives, and here is what we tried:
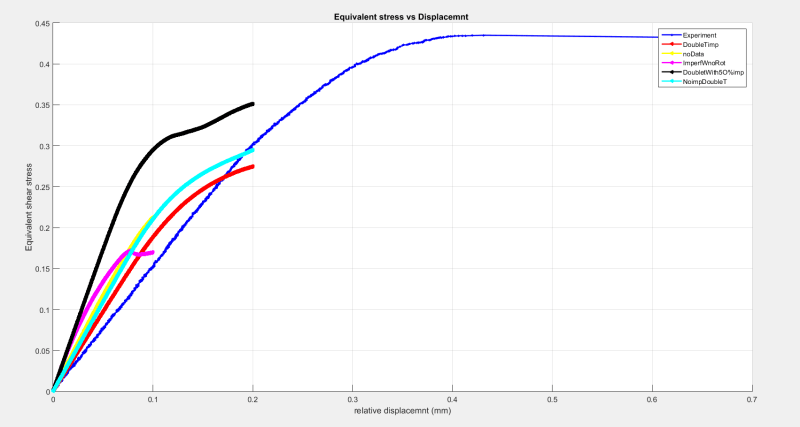
1. Geometric imperfections. They did affect stiffness, but not anywhere near the magnitude required to get a match.
Note: the OP didn't post any pictures of the real-world specimen here so I won't either, but saying that the structure has "geometric imperfections" is understating how irregular and distorted this hexcore was at the end of its manufacturing process.
2. Full model. At first the analysis was done using a "unit" cell, but that raised the suspicions mentioned in this thread, so we modeled the whole core and got rid of analytical "equivalent area" calculations. Still no match.
3. Geometric refinement. We implemented things like curved hexagonal cell corners (no change in results) and experimented with single/double wall thickness (there was some miscommunication here). No cigar.
All throughout our investigation I kept bringing up to the OP the possibility that the experimental data was "wrong" (meaning it didn't correspond to what we thought it corresponded to), but this wasn't something I could investigate since I'm a remote collaborator. But now, reading back on the replies to this thread, I believe SWComposites nailed it on his first response, which he reiterated several times: the measured displacements are inaccurate. I think this is very likely the reason for the gross mismatch in linear-elastic stiffness, since we've ruled out many other possibilities (except, perhaps, extreme initial geometric distortion).
I thank everyone who contributed to this thread, you guys have taught me a lot. Cheers!