Joaquin Osses
Mechanical
- Feb 21, 2018
- 4
I've been studying this topic for a couple of days now. I started by asking some questions regarding output Torque and gear ratios relations. Now I came with the whole picture and some calculations that I been working on. My goal is to find out if I'm in the right direction, and also point-out relations between equations that I'm not sure of. To make this more clear and clean, I divide the system into three sections; A, T and B.
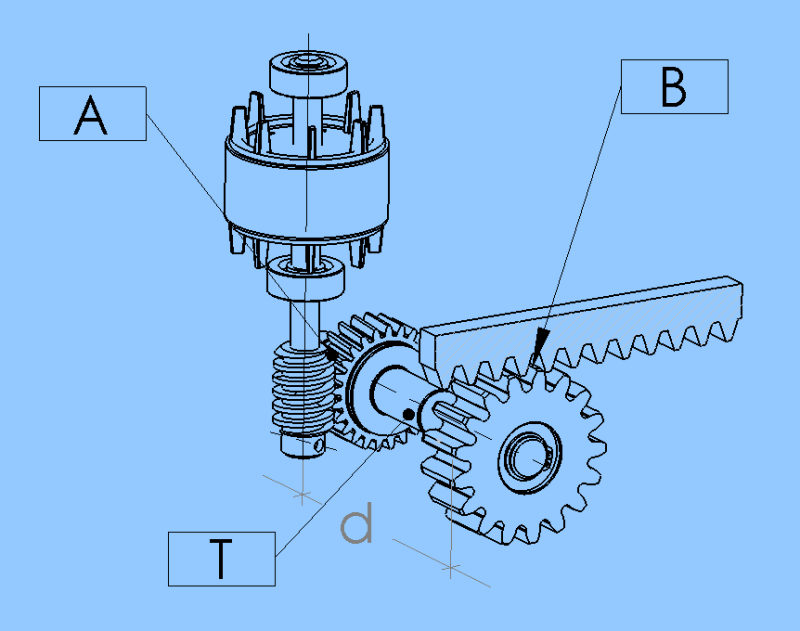
In section A its the electric motor and worm/spur torque transmission.
On another topic with a lot of help, I realise that the power provides by the motor is crucial to generate the output torque and angular velocity that your system requires. No matter the radius, ratios or N of teeth of the spur; if the power isn't enough, the gate won't move at the desired velocity.
So, the problem in question: My goal is to find out if this system will be able to move a gate of 600 kg with a velocity of 0.33 m/s, and how much time it will take to reach that velocity.
The technical data of the motor is:
P = 1/2 hp ; RPM = 1450 ; 220V/50Hz
SECTION A:
P = 0.5 hp = 373 (kg * m2 /s3) Pin = Tin * win
win = 1450 rpm = 151.84 (rad/seg)
Tin = 373 (kg * m2 /s3) / 151.84 (rad/seg) = 2.456 N*m
This, of course, is in an ideal situation, without considering losses. (how can I add an estimation of electric motor losses?)
The worm/spur system has a gear ratio of 23:1.
Considering the efficiency of the system of 80%, we have:
Tout = 23 * (0.8 * Pin) / win = 45.2 N*m
Now, Tout also can be calculated by Tout = 0.8 * Pin / wout
angular velocity applied on the spur is: wout = (0.8 * Pin) / Tout
wout = 0.8 * 373 (kg * m2 /s3) / 45.2 N*m = 6.6 rad/sec --> 63 rpm
To consider real circumstances, its the moment of inertia has something to do within this case? I mean, is this Tout enough to accelerate the spur to 63 rpm??
SECTION T:
In this section, I'm wondering what happens with force transmitted in the distance "d" to the pinion. I'm not sure if I need to consider losses in this section.
SECTION B:
Here I have a lot of question about what's happening. The Pinion has 17 teeth and is module 4.
From gear design, I understand that module, and axial pitch determines the Lead and lead angle of the gear. This has a direct relation with the surface contact (involute) in the system and frictional forces.
Is the torque Tout the same as calculated for the worm/spur system? What about the radius of the pinion? If I increase the radius, the Torque will increase as well? The radius of the pinion is = 0.025 (m)
Tout = F * r
F = 45.2 N*m / 0.025 m = 1808 N
Does this mean that the force applied to the rack is 1808 N? Is this force enough to accelerate until 0.33 m/s?
F = m * a = 600 kg * 9.8 m/s2 = 5880 N ; here I need to consider a friction factor according to the wheels and ground. (0.1)
F = 5880 N * 0.1 = 588 N; this means that I need to generate 588 N force to move the gate, but what about the acceleration? if the gate has 4 m, how much time will take to reach the 0.33 m/s
I need a last push to understand this system entirely.

In section A its the electric motor and worm/spur torque transmission.
On another topic with a lot of help, I realise that the power provides by the motor is crucial to generate the output torque and angular velocity that your system requires. No matter the radius, ratios or N of teeth of the spur; if the power isn't enough, the gate won't move at the desired velocity.
So, the problem in question: My goal is to find out if this system will be able to move a gate of 600 kg with a velocity of 0.33 m/s, and how much time it will take to reach that velocity.
The technical data of the motor is:
P = 1/2 hp ; RPM = 1450 ; 220V/50Hz
SECTION A:
P = 0.5 hp = 373 (kg * m2 /s3) Pin = Tin * win
win = 1450 rpm = 151.84 (rad/seg)
Tin = 373 (kg * m2 /s3) / 151.84 (rad/seg) = 2.456 N*m
This, of course, is in an ideal situation, without considering losses. (how can I add an estimation of electric motor losses?)
The worm/spur system has a gear ratio of 23:1.
Considering the efficiency of the system of 80%, we have:
Tout = 23 * (0.8 * Pin) / win = 45.2 N*m
Now, Tout also can be calculated by Tout = 0.8 * Pin / wout
angular velocity applied on the spur is: wout = (0.8 * Pin) / Tout
wout = 0.8 * 373 (kg * m2 /s3) / 45.2 N*m = 6.6 rad/sec --> 63 rpm
To consider real circumstances, its the moment of inertia has something to do within this case? I mean, is this Tout enough to accelerate the spur to 63 rpm??
SECTION T:
In this section, I'm wondering what happens with force transmitted in the distance "d" to the pinion. I'm not sure if I need to consider losses in this section.
SECTION B:
Here I have a lot of question about what's happening. The Pinion has 17 teeth and is module 4.
From gear design, I understand that module, and axial pitch determines the Lead and lead angle of the gear. This has a direct relation with the surface contact (involute) in the system and frictional forces.
Is the torque Tout the same as calculated for the worm/spur system? What about the radius of the pinion? If I increase the radius, the Torque will increase as well? The radius of the pinion is = 0.025 (m)
Tout = F * r
F = 45.2 N*m / 0.025 m = 1808 N
Does this mean that the force applied to the rack is 1808 N? Is this force enough to accelerate until 0.33 m/s?
F = m * a = 600 kg * 9.8 m/s2 = 5880 N ; here I need to consider a friction factor according to the wheels and ground. (0.1)
F = 5880 N * 0.1 = 588 N; this means that I need to generate 588 N force to move the gate, but what about the acceleration? if the gate has 4 m, how much time will take to reach the 0.33 m/s
I need a last push to understand this system entirely.
