MILRAD
Structural
- Feb 2, 2020
- 18
I have been modeling restrained retaining walls in EnerCalc with the attached geometry. (I hope I uploaded the figures correctly.)
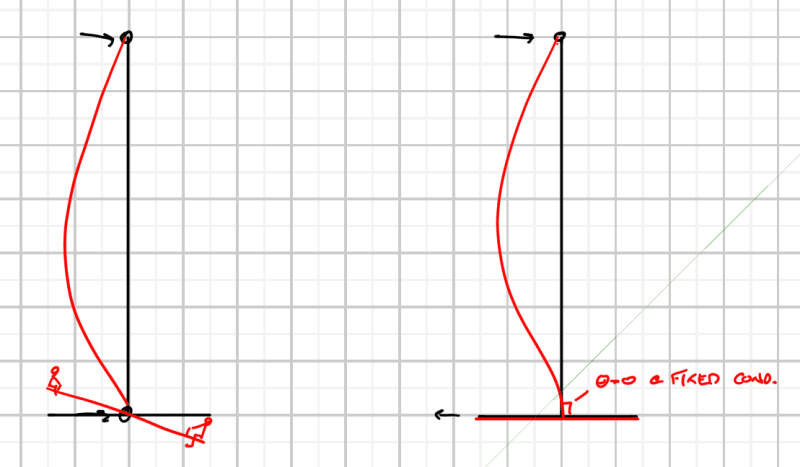
EnerCalc has two options - one where the wall is pinned-pinned and another where the wall is fixed-pinned (fixed at the footing).
When I run the model as pinned-pinned I get the attached results. All of these results make sense - the moment and shear in the wall, the reaction at the top, and the bearing pressure. The triangular distribution of bearing pressure is because of the moment caused by the unequal weights of the soil over the toe and the soil over the heel.
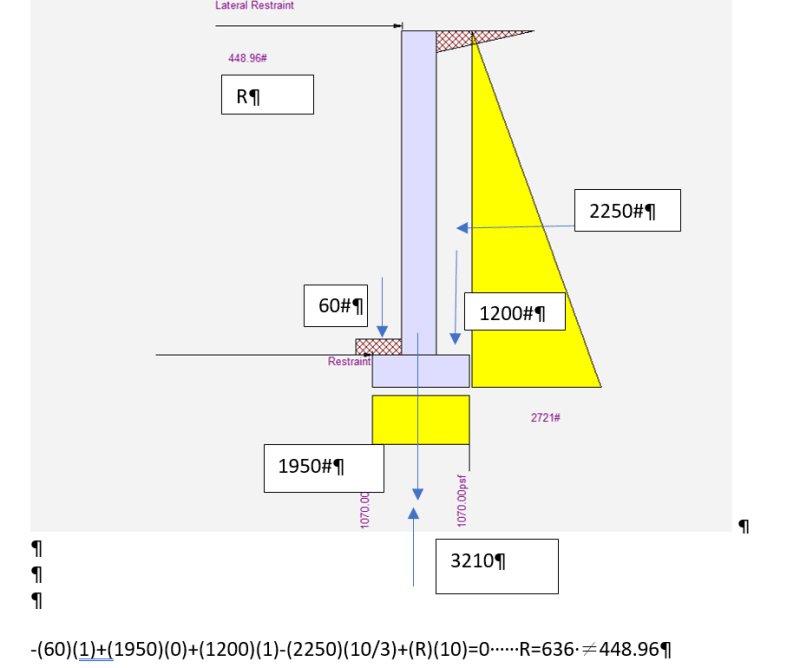
When I run the model as fixed-pinned I expect to see a triangular distribution of bearing pressure to resist the moment caused by the unequal weights of soil and the moment from the the lateral load of the soil less the moment from the reaction at the top (the end moment of a propped cantilever). Instead I get an uniform distribution. The resultant of the bearing pressure equals the weight of the soil, footing, and wall. The reaction, shear, and moment in the wall are what you would get from the statics of a propped cantilever beam with a triangular load.
If I change the lateral pressure and/or the density of the soil I will get the same type of answer - a uniform distribution of bearing pressure equal to the weight and the moments and shears for a propped cantilever.
What am I missing or are the results wrong and the bearing pressures should be triangular?
EnerCalc has two options - one where the wall is pinned-pinned and another where the wall is fixed-pinned (fixed at the footing).
When I run the model as pinned-pinned I get the attached results. All of these results make sense - the moment and shear in the wall, the reaction at the top, and the bearing pressure. The triangular distribution of bearing pressure is because of the moment caused by the unequal weights of the soil over the toe and the soil over the heel.
When I run the model as fixed-pinned I expect to see a triangular distribution of bearing pressure to resist the moment caused by the unequal weights of soil and the moment from the the lateral load of the soil less the moment from the reaction at the top (the end moment of a propped cantilever). Instead I get an uniform distribution. The resultant of the bearing pressure equals the weight of the soil, footing, and wall. The reaction, shear, and moment in the wall are what you would get from the statics of a propped cantilever beam with a triangular load.
If I change the lateral pressure and/or the density of the soil I will get the same type of answer - a uniform distribution of bearing pressure equal to the weight and the moments and shears for a propped cantilever.
What am I missing or are the results wrong and the bearing pressures should be triangular?