EngineerMickeyMouse
Structural
- Jan 15, 2015
- 44
Hi folks,
This time I would like to ask about your opinion.
Below figure is self-explaining, you may notice 150 MPa applied to the tip of smaller solid object (lets assume it is mild steel) and below, larger box is providing supports. Assuming it is converged enough, in this simple example it is obvious real structure will "see" stress about 150 MPa in zone abutting to the larger object. But if the geometry would be more complicated, how would you be so sure how to get rid off this singularity? In other words, how to convince somebody that looking at stress range singularities are not real? I prefer to use stress linearization. What is your opinion? Please share.
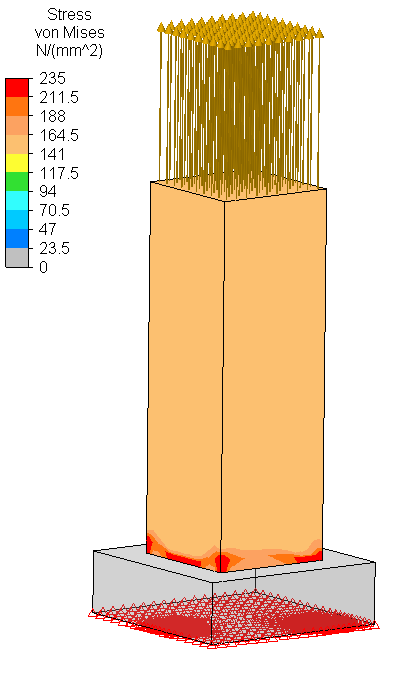
This time I would like to ask about your opinion.
Below figure is self-explaining, you may notice 150 MPa applied to the tip of smaller solid object (lets assume it is mild steel) and below, larger box is providing supports. Assuming it is converged enough, in this simple example it is obvious real structure will "see" stress about 150 MPa in zone abutting to the larger object. But if the geometry would be more complicated, how would you be so sure how to get rid off this singularity? In other words, how to convince somebody that looking at stress range singularities are not real? I prefer to use stress linearization. What is your opinion? Please share.


![[evil] [evil] [evil]](/data/assets/smilies/evil.gif) ), you can provide your understanding in detail like explained as above.
), you can provide your understanding in detail like explained as above.![[smile] [smile] [smile]](/data/assets/smilies/smile.gif) ?
?