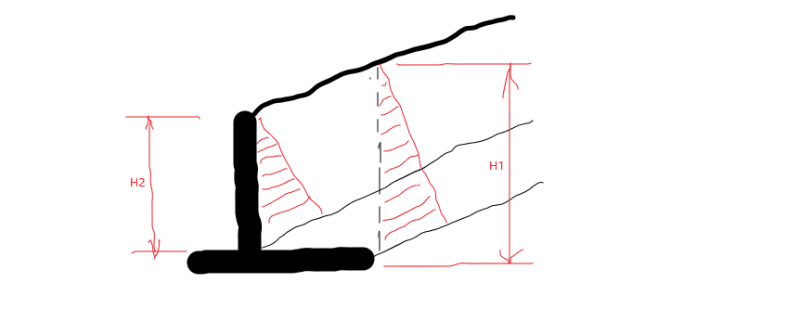
Hi everyone, I am having a debate with another engineer and i want your thoughts.
I am using Coulombs Theory to calculate the Total Active Pressure, Pa acting on the retaining wall shown in the picture.
1st step:
calculate the coulombs active pressure coefficient, Ka which is 0.556
2nd step:
calculate the Total Active Pressure, Pa:
Pa = 0.5KaγH2
Ka is the coulombs active pressure coefficient = 0.556
γ is the unit weight of retained soil = 20kN/m3
H is the height of the retained soil
My question is, what shall i use for height of the retained soil, H in the equation above? H1 or H2 (see picture)
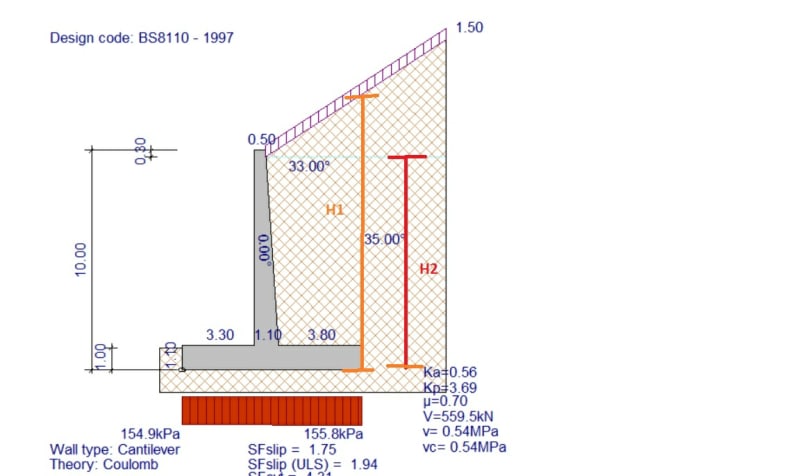
I am using Coulombs Theory to calculate the Total Active Pressure, Pa acting on the retaining wall shown in the picture.
1st step:
calculate the coulombs active pressure coefficient, Ka which is 0.556
2nd step:
calculate the Total Active Pressure, Pa:
Pa = 0.5KaγH2
Ka is the coulombs active pressure coefficient = 0.556
γ is the unit weight of retained soil = 20kN/m3
H is the height of the retained soil
My question is, what shall i use for height of the retained soil, H in the equation above? H1 or H2 (see picture)