Retaining Wall Footings (For the Fourth!) - Fixed or Pinned Base

[Guastavino]

In honor of a fantastic previous thread: Link

So, I have modeled this condition. See attached RISA-3D file. So, I believe it shows that the footing WILL transfer moment to the soil, and quite easily. So, I will go back to the original question lion asked, and say, can we live with that, or should we adjust the design methods?

Backdrop:
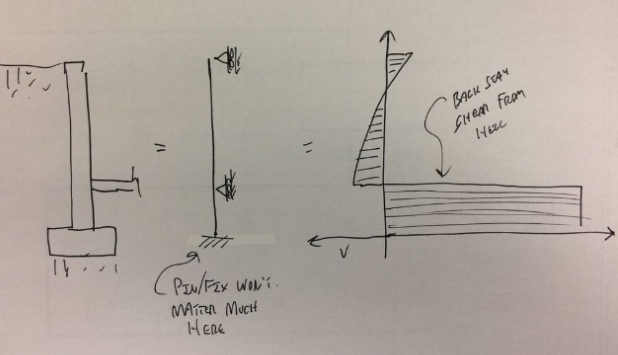
1. Pin-pin wall conditions for RESTRAINED retaining walls is conservative for the WALL rebar. No need to argue this.
2. Pin-pin wall conditions for RESTRAINED retaining walls is NOT conservative for the footings. The additional moment transfers to the footing and increases soil pressure.
3. Many in the previous thread assumed that soil spring stiffness, etc. was not that significant compared to stiffness of the footing/wall.
4. Respectfully, I challenge that assumption and present the attached model as evidence.
5. Intuitively, this also makes sense because to me, the stiffness of soil compared to a footing is still quite large.
6. I open the floor for debate as to what methods to use. It makes a HUGE difference in footing size, which means cost, and it may not have an advantage.

With that said, please no, "WELL, We've always done it that way and there haven't been problems" arguments. It's not that I don't care about that argument, it's just that I want to understand the behavior, not justify the design based on empirical experience (even though it has value).

Thanks to all and I hope for some great discussion.

ALSO, know that RISA-Foundation (Josh Plummer please feel free to comment!), does this method. IE, they transfer footing from the base into the soil and design the footing accordingly, leading to larger footings. Albeit, it doesn't model the soil springs, just assumes the moment transfers. The 3D model that is attached is a plate model has been created to simulate the soil springs.

 

[Guastavino]

Haha, my point is that RISA is one of the top, if not the top, selling structural program. A lot of folks use it to design retaining walls. Therefore, there are a LOT of folks that would be designing that way.

I don't want to be convinced of anything other than best practices. Facts are stubborn things. It just happens that art isn't, and there is an art to structural engineering. I just want to challenge the norm of Pin-pin for a minute to make sure it's an acceptable method. I could argue it either way. Nothing in this thread has convinced me that pin-pin is the best method, and nothing has convinced me that it's not acceptable. I just did a model that appears to indicate that the ACTUAL behavior is likely closer to pin-fixed. Everyone else has suggested things that intuitively make sense, like "the soil will give some and release moment", etc. but my model appears to indicate otherwise.

As for Falzur Kahn, I don't know of them, but I may have seen their work without knowing who they are. I do know that that detail is not impressive to me. I also know that a good and thorough engineer should have caught that detail. I would also note that any half decent architect can cover up a multitude of structural errors with some nice finishes. I say that to say that just because it's a "nice building" doesn't mean it's designed correctly.

 

[KootK]

I just did a model that appears to indicate that the ACTUAL behavior is likely closer to pin-fixed.

I still feel as though the point that I was trying to make with the wonky detail is slipping under the radar. I'll take another stab at it:

If there's a slab on grade and it's not specifically designed to NOT provide lateral restraint to the wall, then pin-fixed is not much closer to the actual behavior than pin-pin. The actual behavior may well be closer to one of the models shown below. And that would lead to back-stay shear that you'd need to reinforce for. So, in summary, my point is that the "actual behavior" path may lead you:

1) somewhere pretty undesirable in terms of your competitiveness;
2) somewhere not necessarily in line with the RISA results anyhow and;
3) somewhere where you won't find many Romans around to keep you company.

In my opinion, the RISA results are just one alternative among several, and not just pin-pin.

Are you interested in any in-print stuff that suggests pin-pin? I'm happy to go digging in my collection but I don't want to expend the effort if you're only interested in the theoretical aspect of this. Even if I can find published examples of pin-pin, I very much doubt that they'll go into the kind of theoretical detail that we've been discussing here.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[canwesteng]

I'm not sure I'm onside with that shear diagram. Seems correct if you assume the top pin is a force to be resisted at the top of the wall, not as if it were a support resisting the force below. Maybe I'm off though, see my fbd.

 

[jayrod12]

Triangular stress distribution is where I think the difference in your two FBDs comes in. Koot's assumes triangular ( I actually think I see a curved shear diagram between the main floor and the slab, he's one to use a straight edge, or straightish at least, if it were a rectangular stress distribution)

 

[canwesteng]

I don't that fundamentally alters the problem though. Imagine you have a beam supported at both ends, and you add a new support some distance x from the other supports. I don't think there is a situation where this can increase your shear, you aren't adding load. Koots sketch looks like load applied to a cantilievered portion of beam. I can see the logic - you take a beam cantilevering some distance from two supports, the shear diagram looks much like that. You add a support at the top though and the two supports at the bottom are no longer required to be a couple to satisfy statics.

 

[JoshPlumSE]

I'm a little late reading this thread. As, I didn't realize it had anything to do with RISA.

I'll start out by saying that I have no opinion on the "right" way to model basement walls. All connections are somewhere between pinned and fixed. But, we will typically use our engineering judgment to say that it's one or the other. So, as long at the foundation details back up your assumptions / judgment you should be fine.

As to reason why the RISAFoundation retaining walls work the way do, I can only point towards a natural "evolution" of the program. When we first added retaining walls they were purely stand-alone cantilever walls. Our users liked them, but then immediately requested that we add on option to pin them at the top where they might connect to a floor slab or diaphragm or such. So, we added the pinned top - bottom fixed option. The natural next step from a pure cantilever wall.

Now, we've gotten some requests for pinned top - pinned bottom walls. That doesn't seem like an unreasonable option to me. It's not the type of structure I've worked on before. But, the industrial world (where I spent most of my design life) is often different from commercial and residential buildings.

 

[KootK]

Exactly as Jayrod explained it. I guess that, technically, there should have been a slight curve to the "big shear" part of the diagram as well but that is of little consequence.

@Canwest: try this in your head (or in SAP) and let me know if it doesn't check out:

1) Start with a 10' beam fixed at the left and pinned at the right.

2) Apply a uniform load of any intensity.

3) Instead of conventional fixity at the left end, extend the beam 6" to the left and provide another pinned support there. All three supports are now pinned.

4) Review your moment and shear diagrams. The original span diagrams should remain essentially unchanged. Shear should skyrocket over the 6" extension.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[Guastavino]

Are you interested in any in-print stuff that suggests pin-pin? I'm happy to go digging in my collection but I don't want to expend the effort if you're only interested in the theoretical aspect of this. Even if I can find published examples of pin-pin, I very much doubt that they'll go into the kind of theoretical detail that we've been discussing here.

Sure, but don't spend more than 5 mins on it. A suggestion of a good foundation reference book would likely suffice. The references I have to date have sufficed to date, but the current project I'm working on requires a bit more involvement.

Thanks to all

 

[hokie66]

When you trench a wall into rock to provide fixity at the base, which I am thinking is what is represented by the section (by someone) that KootK posted, you don't get a support at the bottom, but rather a distributed force over the embedded part of the wall. Not quite as severe for shear as the uniform shear assumption.

 

[KootK]

In seven foundations books, I found several examples of basement walls designed as pin-pin but not a single example of the footing being addressed in concert with the wall. Utterly inconclusive.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[Guastavino]

In seven foundations books, I found several examples of basement walls designed as pin-pin but not a single example of the footing being addressed in concert with the wall. Utterly inconclusive.

Haha, no big surprise there. If anything, this thread has convinced me that we don't really know the true behavior, but be consistent in your design assumptions.

 

[canwesteng]

Here is the shear diagram with the fixed support, I find the max shear to be ~19 kip for some fictional load.

 

[canwesteng]

Here is the shear diagram without the slab as a point of support. I get max shear in the beam of ~28 kip for the same fictional load

 

[KootK]

It's all about the span:backspan ratio which is why I recommended 20:1 above for the experiment. As the space between the two supports representing fixity tends to zero, the shear in the back span tends to infinity.

To an extent, you can think of an analogous cantilever having a cant span matching the distance to the inflection point in the real span. You'd need the fictitious cantilever distance to be several multiples of the backspan before you'd see critical shears in the back span. In your example that ratio appears to be only about two.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[canwesteng]

I understand where you're coming from and it holds true for cantilever with two pins and a small backspan, and to a lesser extent to a cantilever with one pin and one fix support on the backspan, but that is substantially different to what is happening here, as there is no cantilever. As a thought experiment, look at the second shear diagram posted. How will adding a support at any point increase the shear?

FWIW, the first example had a 5:1 ratio. I've bimped it to 50:1, and the shear is now around 23 kips for the same load. As the pin approaches the fixed support this value will eventually reach the ~27 kip that we saw when the pin wasn't there.

 

[KootK]

As for Falzur Kahn, I don't know of them, but I may have seen their work without knowing who they are.

Fazlur Khan <> Firm. Fazlur Khan = Man. A structural engineer not being familiar with Khan is a bit like a lumberjack not being familiar with Bunyan. If you're a reader, I'd recommend picking up his autobiography, written by his daughter who is also a structural engineer (Link). It's probably the most inspiring trade publication that I've ever read and is sprinkled with all manner of technical goodies. For anyone even remotely interested in structural engineering, it reads like blueberry waffles eat: fast and joyously.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[KootK]

I did a little moment distribution in order to validate my position. At at backspan of L/10, I get a 227% increase in shear over the base case. At L/20, it goes to 476%. Granted, attempting hand calcs is a pretty reliable way to embarrass oneself. I await the onslaught.

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[canwesteng]

I need a lot more time to digest this. In FEA the results are what I'd expect, a reduction in shear of ~10% for the case you show, then I use the method of superposition and get an increase of 220%.