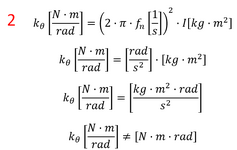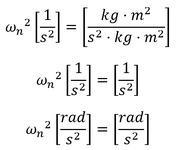Hi all,
I have this doubt when it comes to estimating a rigid body rotational stiffness from a eigen frequencies analysis.
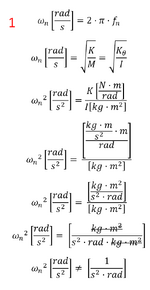
At first it seemed straightforward to me, using the fundamental dynamics equation w_n = sqrt(K/M), where w_n = f_n · 2 · PI
However, I seem to be reaching a unit disagreement issue that I have not found a satisfactory solution to.
Reverting to the spring equation, F = K · x
In terms of rotation, x would be the angle in radians and F would actually be a moment (so F = N.m).
This results in K having units of N.m/rad, which seems consistent.
Going back to the dynamic equation, it seems correct to me that in terms of rotation, mass is to be replaced by inertia:
w_n [rad/s] = sqrt(K [N.m/rad] / I [kg.m^2])
Solving the RHS results in:
sqrt(1/(rad · s^2 )) = 1/(rad · s)
When on the LHS w_n is in units of rad/s
Alternatively, if one was to define the inertia in terms of [kg.m^2/rad], the RHS simple ends up in Hz
I've tried searching similar discussions, but most seem centred on "linear" stiffness
I also found one published paper (Journal of Sound and Vibration) where a more complex analysis is carried, accounting for mass eccentricities: https://www.sciencedirect.com/science/article/abs/pii/S0022460X20301528
However, it sheds little light on the unit agreement as it uses the dynamics equation and specifies inertia in terms of [kg.m^2], with a final result for the rotational stiffness in terms of [N.m/rad]:
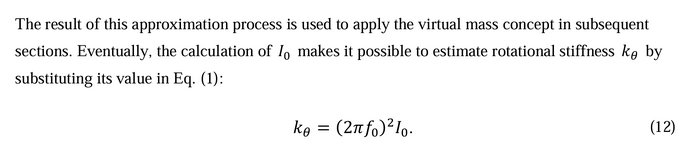
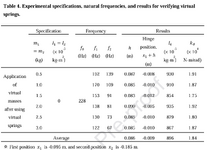
Now, I do realize that at the end of the day radians is a dimensionless unit (hence why rad^2 or sqrt(rad) = rad), but is this something that one just have to live with (sqrt(k/I) = rad/s), or is there something I'm missing?
I have this doubt when it comes to estimating a rigid body rotational stiffness from a eigen frequencies analysis.
At first it seemed straightforward to me, using the fundamental dynamics equation w_n = sqrt(K/M), where w_n = f_n · 2 · PI
However, I seem to be reaching a unit disagreement issue that I have not found a satisfactory solution to.
Reverting to the spring equation, F = K · x
In terms of rotation, x would be the angle in radians and F would actually be a moment (so F = N.m).
This results in K having units of N.m/rad, which seems consistent.
Going back to the dynamic equation, it seems correct to me that in terms of rotation, mass is to be replaced by inertia:
w_n [rad/s] = sqrt(K [N.m/rad] / I [kg.m^2])
Solving the RHS results in:
sqrt(1/(rad · s^2 )) = 1/(rad · s)
When on the LHS w_n is in units of rad/s
Alternatively, if one was to define the inertia in terms of [kg.m^2/rad], the RHS simple ends up in Hz
I've tried searching similar discussions, but most seem centred on "linear" stiffness
I also found one published paper (Journal of Sound and Vibration) where a more complex analysis is carried, accounting for mass eccentricities: https://www.sciencedirect.com/science/article/abs/pii/S0022460X20301528
However, it sheds little light on the unit agreement as it uses the dynamics equation and specifies inertia in terms of [kg.m^2], with a final result for the rotational stiffness in terms of [N.m/rad]:
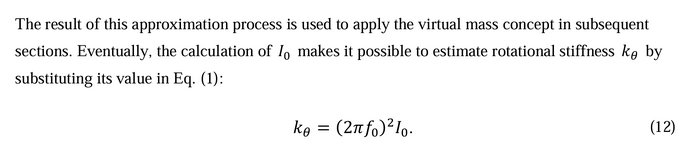

Now, I do realize that at the end of the day radians is a dimensionless unit (hence why rad^2 or sqrt(rad) = rad), but is this something that one just have to live with (sqrt(k/I) = rad/s), or is there something I'm missing?
Last edited: