Lhi
Geotechnical
- Nov 22, 2019
- 8
Hi,
I work in a French office and I have questions about foundation design with EC7 and EC2.
I'm studying column foundations with eccentricity to program an Excel sheet.
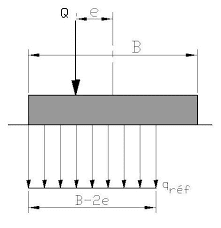
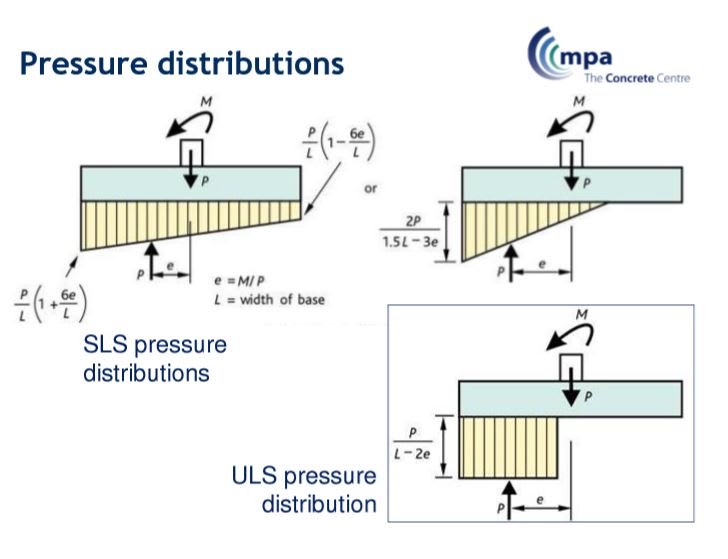
I configured Meyerhoff, trapezoidal and triangular pressure distribution for combined bending to verify the soil pressure under foundations.
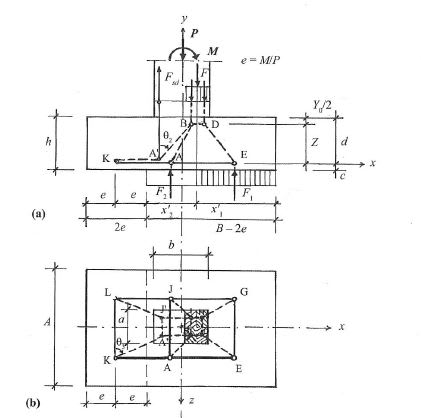
Now I'm programming the reinforcement which is define by struts and ties method if the footing is rigid or bending moment if it’s not the case.
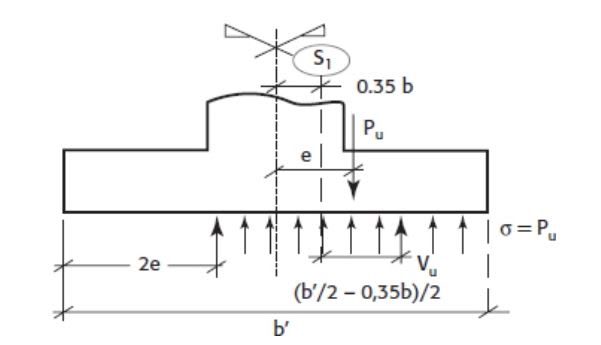
I found in several documents that the reinforcement in ULS is calcultated with a rectangular distribution of the pressure which means Meyerhof's method. But I don't know why.
In fact, with EC7 the pressure under the footing is verified with SLS and ULS. So, we usually start to verify SLS before ULS with EC7.
If we choose the triangular or trapezoidal method (depending on the value of eccentricity) for SLS to otpimize cross sections, is that correct to verify with Meyerhof in ULS? Is it not strange to mix the 2 methods even if SLS is an elastic calculation and ULS a plastic one? Or can we verify ULS with trapzoidal or triangular diagrams? And what about reinforcement? Is it correct to use Meyerhoff's method in SLS?
What is the best engineering practice?
Thank you in advance for your help, I'm a little bit confused about the choice of diagrams..
I work in a French office and I have questions about foundation design with EC7 and EC2.
I'm studying column foundations with eccentricity to program an Excel sheet.
I configured Meyerhoff, trapezoidal and triangular pressure distribution for combined bending to verify the soil pressure under foundations.
Now I'm programming the reinforcement which is define by struts and ties method if the footing is rigid or bending moment if it’s not the case.
I found in several documents that the reinforcement in ULS is calcultated with a rectangular distribution of the pressure which means Meyerhof's method. But I don't know why.
In fact, with EC7 the pressure under the footing is verified with SLS and ULS. So, we usually start to verify SLS before ULS with EC7.
If we choose the triangular or trapezoidal method (depending on the value of eccentricity) for SLS to otpimize cross sections, is that correct to verify with Meyerhof in ULS? Is it not strange to mix the 2 methods even if SLS is an elastic calculation and ULS a plastic one? Or can we verify ULS with trapzoidal or triangular diagrams? And what about reinforcement? Is it correct to use Meyerhoff's method in SLS?
What is the best engineering practice?
Thank you in advance for your help, I'm a little bit confused about the choice of diagrams..