Shear Deformation - Point Moment 7

[Celt83]

This is probably something that is very easy and I am way overthinking it.

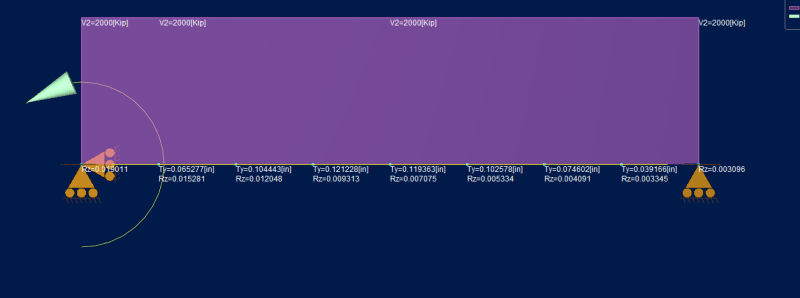
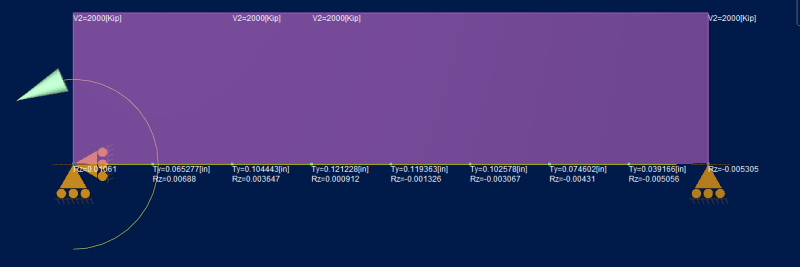
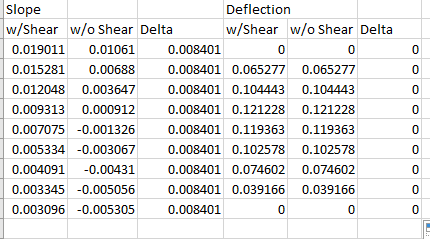
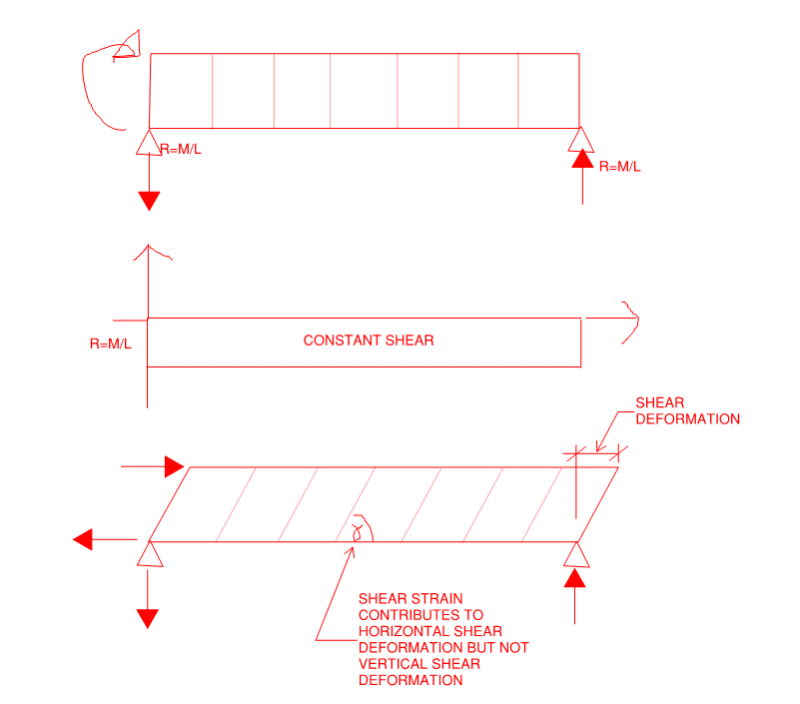
I've done the unit force method which shows that the shear deformation from a point moment is 0 at all locations on a simple span. I've done the same thing to show that the shear component of the slope at any location on the beam is constant = k M / A G L. Here is where I get hung up if the slope is constant and non-zero why is the deflection 0 from a math stand point, the mechanics make sense to me but I'm lost in the math on this one.

I have a great mechanics of materials book by Timoshenko and Young which for me so far has the best break down of shear deformations I've been able to find and in there they present that the slope due to shear is simply dy/dx = tau,max / G = k V_x / A G, which aligns with my unit method solution of k M / A G L.

integrating that once yields: y,shear = k M x / G A L + C1

Initial conditions are x=0, y=0 and x=L, y=0 the first condition yields C1 = 0, however the second condition yields C1 = k M / A G ... so I get that something is missing here which would should result in y,shear = 0 but I am at a loss.

would greatly appreciate any insight on this one.

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[JGard1985]

In your first integration, looking at your first integration of shear aren't you missing the +C constant shear. The shear diagram is flat with a height of M/L.

I dont think C1=0 in your first condition.

Jeff
Pipe Stress Analysis
Finite Element Analysis

http://www.xceed-eng.com

 

[Celt83]

The V_x in the equation from Timoshenko is shear in a small differential section which would be constant in the point moment case, so V_x = M / L.



Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[Celt83]

Realized I botched my sign convention on the unit force derivations, answers remain unchanged though:

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[rb1957]

"I've done the unit force method which shows that the shear deformation from a point moment is 0 at all locations on a simple span."

how can this be true ? the point moment is reacted by a couple (at the reactions), therefore there is shear in the beam.

why use unit force method on a statically determinate beam ?

I don't understand what the two sketches on the RH mean ? It looks like you're calculating reacting for a unit shear applied at a point a ?

On the LH it looks like a 1/2 hearted attempt to calculate slope …

Lay out your calc clearly so we can follow …
with M applied at A, the reactions are Rb = M/L and Ra = -M/L
the moment in the beam is M(x) = M-Mx/L
then v(x) = int M(x)/EI = M/EI*(x-x^2/2L) + C
and d(x) = int v(x) = M/EI*(x^2/2-x^3/6L) +Cx+K
d(0) = d(L) = 0 … K = 0 and CL = -M/EI*(L^2/3)
then v(x) = 0 at x-x^2/2L-L/3 = 0 … x^2-2Lx+2L^2/3 = 0 … x = L(1-1/sqrt(3))

or something like ...

another day in paradise, or is paradise one day closer ?

 

[Celt83]

@rb1957:

you've gone thru the derivation of the slope and deflection due to bending, I am looking specifically at the shear deformation.

I've verified my constant slope due to shear = k M / G A L and deflection due to shear = 0 with various text sources and software. Problem with the text sources is the info is simple shown as a table of values associated with load types and there is no actual derivation or explanation provided.

W/ Shear Deformation:

W/O Shear Deformation:

Delta between the two:

Computer Calculation Parameters:
L = 5 ft
M = 10000 kip*ft
Beam is a W36x135 - k / A G = 4.18x10^-6 kip (A/k = web area = 21.36 in^2 and G = 11200 ksi)

The purple diagram is the internal beam shear


Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[BAretired]

A beam with moment applied at one end deflects due to bending but not due to shear because shear is constant over the entire span. Shear deflection requires a change in shear somewhere along the span.



BA

 

[Celt83]

BA:
Thanks for the response, I think I'm having a hard time grasping what the actual cross section deformation looks like since the slope is changing but the deflection is not between the pure bending case and the bending + shear case, assume there is more warping action going on which is keeping the elastic curve on the same line.

Or is it less warping?


Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[BAretired]

A simple beam with moment acting on it creates a shear M/L which is constant over the span. Plane sections remain plane which means there is no warping anywhere.

I have a great mechanics of materials book by Timoshenko and Young which for me so far has the best break down of shear deformations I've been able to find and in there they present that the slope due to shear is simply dy/dx = tau,max / G = k Vx / A G, which aligns with my unit method solution of k M / A G L.

integrating that once yields: y,shear = k M x / G A L + C1

Initial conditions are x=0, y=0 and x=L, y=0 the first condition yields C1 = 0, however the second condition yields C1 = k M / A G ... so I get that something is missing here which would should result in y,shear = 0 but I am at a loss.

In your first equation: dy/dx = tau,max / G = k Vx / A G, the x is a subscript, i.e. the term should be V_x, not V times x.

There is nothing missing. C1 = -k.M.x/G.A.L. At x=0, y=0. At x=L, y=0. At x = L/2, y=0.


BA

 

[Celt83]

BA agreed the Vx is a subscript not V*x, but V_x=m/l.

The integral is correct:
y = k*m*x / G*A*l + C1

Direct substitution of the first boundary condition yields C1=0, However knowing y=0 at x=0 and x=L it is clear that the only real solution for C1 is that it equals -k*m*x / G*A*l. Sorry my calculus is a bit rusty.

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering

 

[KootK]

There is shear deformation. It's just horizontal in this case rather than vertical.

 

[BAretired]

There is shear deformation. It's just horizontal in this case rather than vertical.

I do not agree with that assessment. Plane sections in the beam rotate but remain plane. Horizontal movement of fibers above and below the neutral axis result from bending, not shear.



BA

 

[jayrod12]

Ah, but BA, there must be horizontal shear in the beam in order for it to resist the bending, and where there is a change in shear, there will be shear deformation.

Or at least I imagine that's the road KootK was thinking..

 

[BAretired]

Ah, but BA, there must be horizontal shear in the beam in order for it to resist the bending, and where there is a change in shear, there will be shear deformation.

Sorry jayrod but neither of those statements is accurate. A beam loaded with an equal and opposite moment M at each end has no vertical shear and no horizontal shear stress but resists bending moment M throughout its length.

Horizontal shear stress at a point is found by: v = VQ/Ib. Horizontal shear stress varies directly with V. There is no warping of the cross section unless V is changing.

BA

 

[KootK]

1) In general, you don't need a change in shear to have shear deformation. All you need is shear. Shear begets shear stress; shear stress begets shear strain; aggregated shear strain begets shear deformation. The conservation of energy makes this pretty much a law.

2) In particular, you do need a change in shear in order to have vertical shear deformation in a simple span member. More specifically, you need a reversal of shear, not just a change in shear. This is really just the satisfaction of a boundary condition when both supports are at a common elevation. If shear deformation takes you off at a particular slope as you leave one support, there's just no way to land at the other support unless you reverse the slope at some point. Note that a cantilever can have a uniform shear diagram and still have vertical shear deformation.

3) The sketch below, studying only the shear component of deformation. shows where the shear deformation goes in Celt83's case. I believe that the source of his mathematical discrepancy may be that the unit load method, being an energy method, should take some account of the energy represented by the shear strain shown below. That energy input, however, will not contribute to vertical shear deformation.

 

[IDS]

This is interesting.

My immediate reaction was that if there was a shear force then there must be a shear deformation, so I asked my computer and it said:
"BA Retired is right (you should have known that)."

But I also checked a cantilever with a point load at the free end, and that has a shear deformation (as KootK said), so what is going on?

I think the important points are, for a beam with constant shear force, and considering only shear deflections:
For any rectangular segment of the beam:
- Both pairs of faces remain parallel
- The change in corner angle is proportional to the shear force
so for constant shear:
- The top and bottom faces must remain straight.
- For a simply supported beam the line between supports remains horizontal, so there will be no vertical shear deflections.
- For a cantilever the fixed end face will remain vertical, so all the vertical faces will remain vertical, but the top and bottom faces will have some constant non-zero slope.

A 2D beam analysis; subtracting flexural results from flexure+shear results, confirms these results:
- A cantilver has constant non-zero slope.
- A simply supported beam has zero vertical deflection, but constant non-zero slope, since the slope is defined by the angle of vertical sections, not the slope of the bottom face (or centre line); see KootK's 3rd section.


Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[BAretired]

@KootK

How do you like your steak...rare, medium, well done or burnt?

 

[KootK]

Medium well and accompanied by baby Yukon potatoes and challenging conversation.

 

[IDS]

To be a bit picky perhaps:

More specifically, you need a reversal of shear, not just a change in shear

is not correct.

Any change of shear will result in the top and bottom face no longer being straight, so there must be some vertical deformation. With a clockwise moment applied at the left hand end, and a downward point load at mid-span, the shear force will always be positive, but there will be a downward shear deflection.

Doug Jenkins
Interactive Design Services

http://newtonexcelbach.wordpress.com/

 

[Celt83]

So here is an odd one take IDS's last post but reverse the point load and give it a magnitude such that the internal shear is 0 between the left support and the point load. Based on superposition the segment with 0 internal shear will undergo shear deformation caused by the applied point load.

Appreciate everyone's responses on this one.

Open Source Structural Applications:

https://github.com/buddyd16/Structural-Engineering