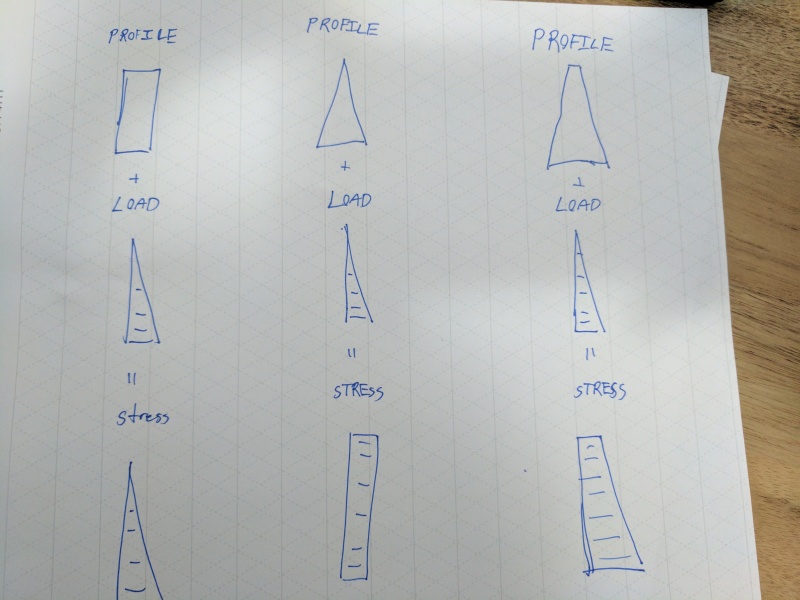
I don't believe that the presence of the axial stress changes anything. By negative superposition, you can strip it out and again deal with the uniform moment as before.
jd said:
I'm still struggling a bit with the thought that the members don't need any connection between layers in this case.
Consider the absurdly trivial yet altogether salient analog of an axially loaded member. Say, 2-2x6 that you'd like to resist an axial load of 1000 lb compositely. Don't sweat buckling or the moments due to eccentricity. Neither is germane to the example. You've got three possibilities:
1) Put all 1000 lb on one of the 2x and do not nail the plies. One ply resists, the other does not, the axial strain profiles of the two sticks do not match, and you have the analog of the non-composite case.
2) Put all 1000 lb on one of the 2x and do nail the plies. Load transfers between plies, each ply resists 500 lb, the axial strain profiles of the two stick match, and you have the analog of the composite case where shear transfer between plies is required.
3) Put 500 lb on each of the 2x and do not nail the plies. No load needs to be transferred between plies, each ply resists 500 lb, the axial strain profiles of the two stick match without any interconnection, and you have the analog of the composite case where shear transfer between plies is not required.
The uniform moment example here is very much like #3.
I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif)