Single Angle Resolving Moments into Principal Axis

[EngTipper.]

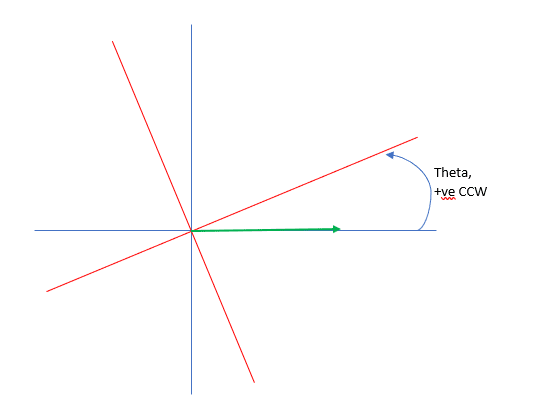
I'm working on an unsupported single angle in bending, and I understand the bending moments about the geometric axis need to be resolved in bending moments about the principal axis.

At this wiki link, there are equations provided to transform a point due to rotation, which is straightforward.

https://en.wikipedia.org/wiki/Rotation_(mathematics)

Where i'm running into issues is that i'm trying to rotate bending moments not points. Say i have a bending about the geometric x-axis Mgx (gravity loading on the horizontal leg, which is at the top) and no applied bending about the geometric y axis (Mgy=0). This causes bending about the two principal axis, Mpx and Mpy. Is what im showing below correct?

Mpx=[Mgx]Cos(theta)-[Mgy]Sin(theta) = [Mgx]Cos(theta)
Mpy=[Mgx]Sin(theta)+[Mgy]Cos(theta) = [Mgx]Sin(theta)

 

[rb1957]

isn't this "just" resolving the moment vector into a rotated axes co-ord system ? A picture saves a thousand words ...

this shows X' = X*cos(theta), Y' = -X*sin(theta) ... no?

If theta is +ve CW (so the angle shown is -ve) then Y' = X*sin(theta)


"Hoffen wir mal, dass alles gut geht !"
General Paulus, Nov 1942, outside Stalingrad after the launch of Operation Uranus.

 

[Denial]

For a discussion on bending about non-principal axes, see
thread507-468425