Singly Symmetric Compact I Shaped Member Bent About Their Major Axis 3

[Deener]

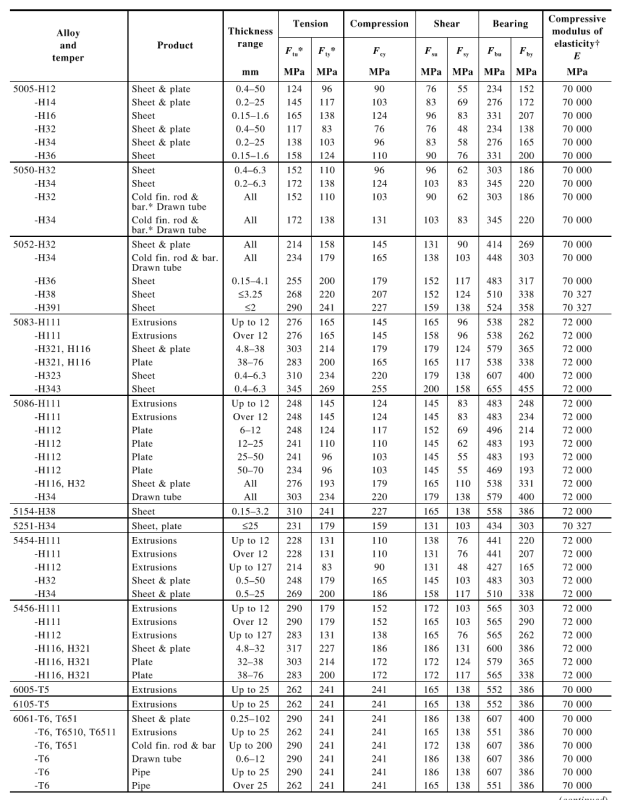
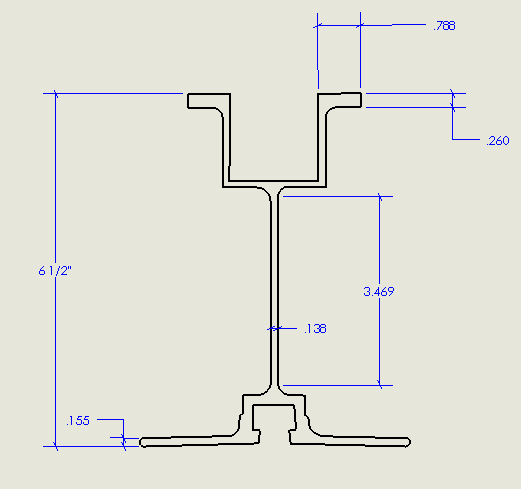
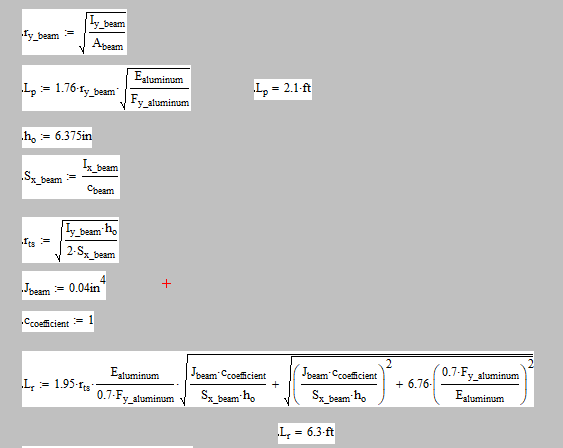
I'm evaluating the flexural capacity of a simply supported 6 1/2" deep Aluma beam with a point load (dead = 170 lbf, Live = 1000 lbf) at mid span (span is 10ft). Assume the beam is braced at end points only. Below is a snapshot of the aluminum beam cross section. Using the dimensions below along with AISC table B4.1b - case 10, and B4.1b Case 15, I can conclude that the top compression flange and web are compact(0.788in/0.260in and 3.469in/0.138in). . Table user note F1.1 in AISC 15th edition (pg 16.1-45) clearly states that the limit states to be checked for this case are yielding and lateral torsional buckling. Since my unbraced length exceeds the limit for inelastic lateral-torsional buckling, I have to use equation F4-3 which includes the critical stress. Now for my questions.
1. There is no documentation for the torsional constant of this beam. I have used a preliminary value for a W-shape (W6x8.5). Is there a way I can calculate this value myself? I'm using SolidWorks for CAD and it doesn't appear to give me this value as a section property.
2. The beam will be simply bearing on the bottom flange at either end. How can I confirm the bottom flanges are stiff enough to restrain this beam against rotation at the points of support as per AISC requirement F1.(b)?
3. If I limit the span of the beam to 6ft, the unbraced length is then between L_p and L_r and the limiting moment becomes dependent upon the plastic section modulus (as well as other variables in equation (F2-2). How can I calculate this value for the custom cross section? I know the ratio between S and Z for W shapes is 1.5. Could I apply that here as well?

Thanks in advance

 

[JStephen]

First off, the AISC limits for compactness, buckling, limiting spans, etc., are all based on steel and not applicable to aluminum. There is an aluminum design manual that you would need.
For the torsional constant, see Roark's Formulas for Stress and Strain. There is an equation for I-beams based on largest inscribed circle, and I believe that can be matched up to the values in the steel manual for steel members. For aluminum members, this may be defined differently, but refer to that design manual to confirm.
You could also have failure modes with the outstanding flanges spreading apart under load that is not normally applicable to I-beams.

 

[phamENG]

My first comment would be to not use AISC for this analysis. The Aluminum Design Manual is your best option. They are set up very similarly, and many of the equations are similar, but it accounts for the subtle differences in material behavior between steel and aluminum.

For the torsional constant, AISC does provide a good torsional design guide. I know I just said not to use AISC, but DG 9 has a lot of solid and fundamental torsional principles in it. I don't have it in front of me, but I believe they go into the derivation of those values.

No, don't use a ratio for S to Z. If you want the plastic section modulus, you need to find the plastic neutral axis: area above = area below. Find the centroid of each area, and multiply the half area of the cross section by the distance between centroids. The idea is this for a perfectly elasto-plastic material: when elastic, your modulus of elasticity is perfectly linear up to yield. After yielding, you have perfectly plastic behavior, so your stress cannot go above yield and strain increases to infinity. So the plastic modulus assumes you have just reached full yielding throughout the cross section. To be in equilibrium, tensile stresses must equal compressive stresses - since the stress level is constant, that means the areas have to be equal. Then, finding the distance between centroids gives you the effective moment arm for the internal resisting moment of the member at the moment of full yielding.

 

[jjl317]

I second PharmENG comments - aluminum is significantly different than steel

Also, in my experience in the concrete shoring world, contractors / suppliers will often generically refer "Aluma Beam", which I believe is what you have shown, but there are many variations of 6 1/2" high aluminum shoring beams (Aluma different than Safway different than Symons, etc.) with different cross sections, flange widths, alloy/temper, etc. so be careful. And most manufacturers have load charts, though they typically wouldn't address a case with a 10' unbraced length.

 

[Agent666]

I think for something so complex using any general formula for section properties comes with the knowledge that it's only ever going to be an estimate and in some cases most likely wrong. Like most things not worked out correctly you'll never know how wrong.

For an accurate estimate of the torsion constant (and other properties you're going to need to jump into evaluation via an FEM approach. Commercial software such as IES shape builder will do it, or if you're after a free alternative this excellent python package will handle it as you can build up a custom shape in either of these packages if you know all the dimensions. If you post a cad file of the profile someone might even do it for you.

Regarding the other stuff people have been answering, 100% agree aluminium isn't the same as steel.

 

[Deener]

Thanks for the comments. I agree that aluminum has different material properties than steel. What's stopping us from substituting in Young's modulus and the yield strength values for aluminum in these AISC equations?I'm guessing it's only the limiting slenderness ratios in Aluminum that I need to know. This is not a fatigue loading scenario and I'm only interested in the ultimate limit state of yielding and LTB. The aluminum design manual looks like a great resource but it's almost $500 USD. I can't justify that for the one job that I'm checking an aluminum beam for. I'm going to suggest a steel beam be used instead. The only other option would be to actually setup this aluminum beam at the required span and test to see what kind of loads it can support before lateral torsional buckling occurs.

 

[phamENG]

It's been a long time since I've had to do an aluminum design, but as I recall several of the equations have modified coefficients and many use the elastic modulus rather than the plastic modulus. The material properties are different, the manufacturing process is different, etc. This results in variable behavior and different initial stress states in the material that alter the design equations. $500 - wow. That's $300 less than the last time I checked.

When you say steel instead of aluminum - do you mean a steel wide flange or similar? That sounds like a good idea. I could be wrong, but I get the impression you're trying to push a proprietary shoring beam beyond the manufacturer's published load tables. I'd only do that if it were the absolute last option.

 

[r13]

1) See the linked paper for calculating torsional constant for monosymmetric shape. Link
3) The ratio between plastic modulus and elastic modulus equal to 1.5 is valid only for rectangular section. See the linked paper on how to calculate the plastic modulus. Link

 

[Agent666]

Deener, aluminium has many more differences in design than steel than just the young modulus.

For one the yield stress is a proof stress, there is no yield plateau, so there is no plastic behaviour in a typical steel sense.

Second lots of the grades of aluminium will have different proof stress levels for design depending on the type of stress your member is under, for example the tensile strength is different to the compressive strength for design purposes.

Thirdly the typical extruded sections are thin, and their design has more in common with cold formed steel than hot rolled steel equations.

Forthly, there are many grades of aluminium, with a wide range of material properties. So you have to be very careful/sure on what you are specifying and receiving.

 

[Deener]

Agent 666 - can you give me your source for saying the tensile strength is different than the compressive strength for aluminum (assuming buckling does not occur)? The CSA design guide says otherwise:

Also, yield stress is stated at the 0.2% offset for steels as well so how is aluminum different there? I get there's a different shape to the stress strain curve. The CSA aluminum design guide uses the yield strength of the material along with the plastic section modulus to check the resistance of a member in flexure. The same method is used for steel. There are many grades of steel as well as aluminum. So if the youngs modulus, yield strength, and limiting slenderness ratios are all accounted for, where are all these remaining many more differences in design than steel for a beam in flexure?

 

[Deener]

phamENG - I have suggested using a steel W flange as you mentioned. From what I understand, the intention of this beam is to mount it to a temporary structure (i.e. scaffolding) so an overhead hoist can be attached to the bottom flange with a beam trolley for lifting. The aluminum beam is preferred since it's lighter. But you're absolutely right. These aluminum beams typically used for formwork are designed for uniform loads and I would guess are typically considered continually braced at their top flange. I'm going to double check bending in the bottom flanges due to the local point load as well as tension in the web. This might be an easy way to rule out the use of this beam.

 

[STrctPono]

I'm going to double check bending in the bottom flanges due to the local point load as well as tension in the web.

You're spot on with this understanding of the behavior. I see so many times in falsework design where rolled or extruded sections that the local bending of the flanges or web due to a non-typical loading condition always cause me to throw up the red flag. Alumabeams have that slotted section where the bottom flange meets the web. That's for installation of the W-clamp, however, I think this makes the beam a poor choice for attachment of a trolley hoist. The presence of the slot creates a detail that is susceptible to bending if the hanging load is too far out on the flange.

Even if you go with a hot-rolled steel beam, whenever they stack beams on top of falsework like that you also want to make sure that the system isn't going to roll and needs to be properly restrained at the ends. Just my 2 cents.

 

[Agent666]

Hi Deener, for example this screenshot is from my own local aluminium design standard (Australian & New Zealand), you'll note for example strength depends on temper and type of design action (and values used vary considerably):-

It could well be your aluminium design standards hides this behind the scenes in the equations, or maybe it neglects it completely, or doesn't take into account any benefit afforded and only uses the lesser value. I'm not familiar with CSA aluminium standard to be honest.

yield stress is stated at the 0.2% offset for steels as well

I disagree with this, the stress/strain relationship is linear for structural (carbon) steel up until the yield plateau. Proof stresses are only really used with materials that are not linear in their stress/strain relationship. Stainless steel is another good example of this in addition to aluminium

By comparison aluminium has no defined yield plateau like steel and generally has a non-linear stress/strain relationship.

 

[Lomarandil]

Why reinvent the wheel here? Why not just call up the manufacturer and get a load table?

----
just call me Lo.

 

[WinelandV]

I second Lo - This is a beam made by someone (aluma-systems), for the purposes of shoring/falsework. These have known capacities at various lengths. If this analysis is just for kicks, go ahead and knock yourself out. Otherwise, get on the horn (um.. that's phone) and start trying to get ahold of the information.

 

[AnimusVox]

You'll need the torsional constant, you can use autocad to provide section properties, although I don't know if you can obtain torsional section properties from it.

Once you have the section properties, I would proceed with chapters B & F of the ADM (for flexure). This would be classified as an open shape, and if it's 2015 IBC or more recent the 2015 ADM requires direct strength method (read: finite element analysis). Our office uses CUFSM ( a finite element analysis software) for this.

If it's the 2012 IBC or older, you'll be using the 2010 ADM where direct strength analysis isn't required.

You'll need to determine the flexural capacity which is the minimum of:

Flat element 1 end supported compression (ADM B.5.4.1)
Flat element 1 end supported flexure (B.5.5.2)
Open shape Flexure (F.2.1)
Local/LTB interaction (F.2.3)

(and, of course, confirm these are all below the yield moment)

I would need the section properties and the alloy & temper for this beam and I could calc it in about 3 minutes (not using direct strength of course, because I don't do FEA for free lol)

 

[Deener]

Agent666 - Thanks for sharing the table. That's useful information. I won't disagree with you about low carbon steels showing a plateau on the stress strain curve. Regardless of how the yield value is obtained, it's still the yield value to use in the design equations. I will be very cautious when confirming the grade of aluminum.
Lomarandil and winelandv - These beams are meant for uniform loads which assume the top flange is continually braced. Having the beam simply supported and unbraced brings up the concern of LTB. I have asked the supplier if they have any loading info for this case but I'm not holding my breath.
AnimusVox - Thank you for directing me to the proper sections of the ADM. Unfortunately I don't have a copy of that but I'm sure the CSA is quite similar. Tough part is figuring out the torsional constant. I'll hopefully take a crack at that this weekend.