Sliding Check for a House Built on A Slope 1

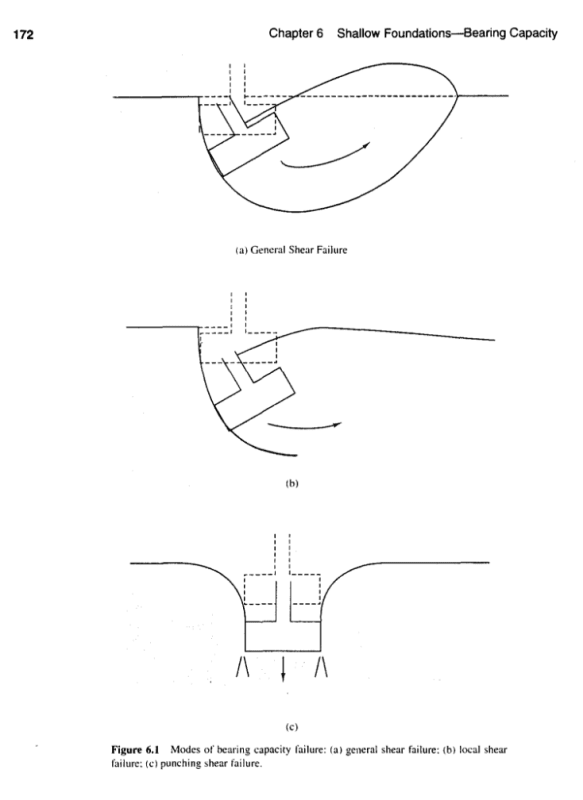
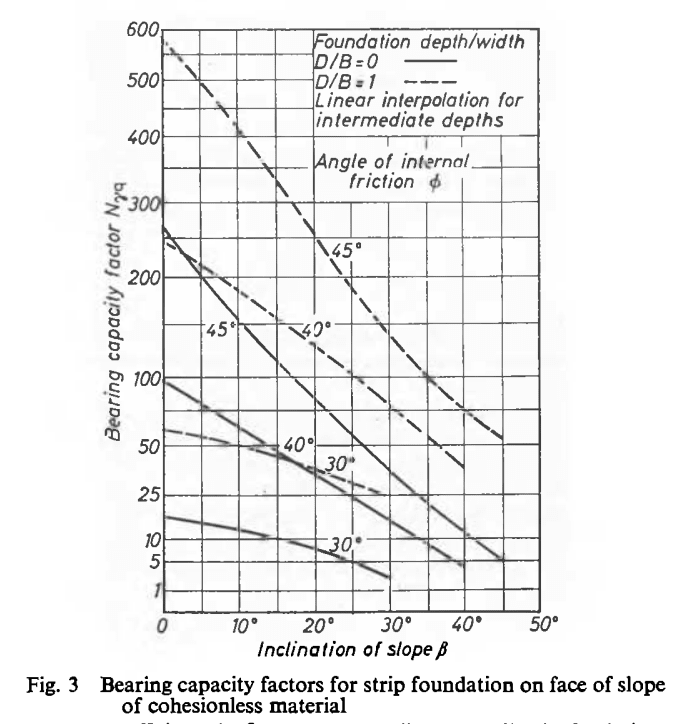
[Yao1989]

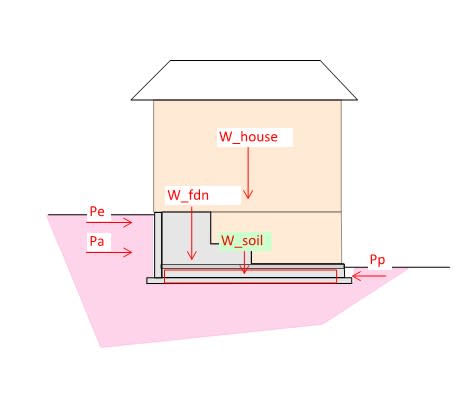
Try to do a quick sliding & overturning check for a house built on a slope.

Pe represents seismic earth pressure
Pa represents active earth pressure

Resisting forces I think will be weight of the house & concreete foundation.
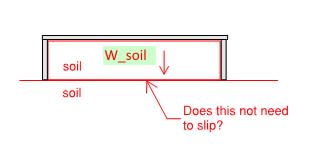
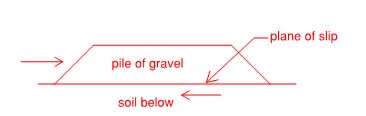
However, my questions is can the soil below the slab on grade but above the bottom of the strip footing (typically 2~3 ft) be considered as force resisting sliding (has to multiply by friction coefficient of course). Technically for the house to move, all the soil below slab on grade but above bottom of the footing will need to overcome sliding before the whole house can move.

Has anyone run into this problem before?

 

[KootK]

At best I think that you get the weight of the SOG times the appropriate coefficient of friction. In order to push the entire soil mass in excess of that would probably require exerting that push into the soil through the foundation wall below the SOG on the left hand side of your sketch. And that would see you limited by a passive soil pressure failure at that location kicking the SOG upwards.

Even taking Pp across the width of your building seems questionable to me as the foundation wall will flex egregiously along that width. You'd likely only mobilize a few feet of wall on either side of any transverse foundation walls.

 

[Yao1989]

So what if diagram is drawn differently like this:

Doesn't it seem that the soil must overcome the weight x friction in order to slide?

 

[HTURKAK]

You may do a quick sliding check with comparing with the slding resistance ,

ΦVc = Φ× friction coefficient × P ( P is total compression force at the bottom of the foundation and Φ is Resistance Factor and equal to 0.85 for Sliding (by either friction or cohesion) , refer to table 12.13-1 Resistance Factors for Strength Design of Soil–
Foundation Interface )

P should be reduced for vertical acc. and P= ∑W(1.0 – 0.4Av)

The frictional resistance and shear resistance sometimes confused and in your second sketch, if the soil inside the perimeter ftg is not disturbed, the continuous ftg will be shear nib and will mobilize the shear str. of the soil. If the soil (pile or gravel) backfilled , in this case, the wt of pile/gravel should be added to the ∑W to find the sliding resistance of the soil below.

In any case, some standards do not allow the friction coefficient, μ GT 0.4 ( μ shall not exceed 0.4)

 

[Guest090822]

You should be more concerned with the soil bearing capacity if the foundation is in a slope. Your capacity is usually cut in half. You should take a look at basic theory.

 

[XR250]

Can you elaborate, TheRick? Never heard of this..

 

[Guest090822]

XR250 - here are a few basic illustrations.

Failure mechanism when not in a slope:

Failure mechanism when in the slope:

You should be able to start with any college textbook explaining the theory, but you can see from the images that in a slope you only have roughly half of the resistance.
This is an important topic and I've rejected many designs over the years with foundations in/on slope that didn't take the situation into account accordingly. A lot of designers fail to read the footnotes at the end of "presumptive" value charts too that often state if the foundation is in/on a slope then the allowable capacity is invalid.

I've seen it more times than I can count over the years.

 

[BridgeSmith]

I'm with KootK on this. You could use the SOG weight, but if the strip footing slides, it doesn't mobilize all of the soil bounded by the footing. At best it may mobilize some passive resistance of the soil against the the inside of the strip footing, as it does on the outside.

However, if you're counting the sliding resistance of the SOG, even that might be 'double dipping' (expecting to same soil to resist forces twice). You could theoretically discount the passive resistance zone from the sliding resistance provided by the slab, but considering that pretty much all of the parameters that go into this calculation are typically rough estimates, that seems like pointless refinement. IOW, if it doesn't work without it, you're cutting it too close, IMO.

You may want to consider if your structure can tolerate the amount of movement required to mobilize the passive resistance you'll be counting on, and if it can, whether you can be absolutely sure that soil you're counting on to provide the passive resistance will be there for as long as the house will be. We generally don't even make that assumption for retaining walls (unless they're like less than 3' high with a sidewalk in front of them).

Rod Smith, P.E., The artist formerly known as HotRod10

 

[chris3eb]

@TheRick

Isn't the top diagram showing that bearing could cause either of those two failure surfaces with equal likelihood, not that they would both occur at the same time? In the bottom diagram, there could be a resistive surface to the upslope direction, but it's only showing the downslope one because that one will be weaker than the upslope one (therefore controlling).

I'm not saying that the slope condition doesn't give you less resistance, but I don't think it's as simple as saying it's half as much.

 

[Guest090822]

chris3eb - take a look at the published material. I've been doing this a long time. The Rule of Thumb is half, but of course you have to determine it via accepted methods. I forget I'm on a forum of engineers and that 0.48 is not 0.50.

Take the advice for what it is, or let the slope fail due to inadequate capacity and explain yourself in court.

If you aren't familiar with the concept then don't speculate.

 

[Yao1989]

@BridgeSmith
With reference to my second post, why doesn't it mobilize all the soil bounded by the footing? If we just have a pile of gravel sitting on asphalt, wouldn't we still need to overcome the friction between the gravel & aspalt (or the internal friction of the gravel) in order for it to slide? How is this different?

 

[KootK]

Doesn't it seem that the soil must overcome the weight x friction in order to slide?

Same answer but with a wildly persuasive sketch this time around:

In order to push the entire soil mass in excess of that would probably require exerting that push into the soil through the foundation wall below the SOG on the left hand side of your sketch. And that would see you limited by a passive soil pressure failure at that location kicking the SOG upwards.

The other thing to consider is that, while load delivered to the bottom of the foundation might be driven through some version of the path that you're imagining, load delivered to the top of the foundation wall will hit the diaphragm there and make it's way through whatever the VLRFS is that stabilizes the diaphragm.

 

[XR250]

chris3eb - take a look at the published material. I've been doing this a long time. The Rule of Thumb is half, but of course you have to determine it via accepted methods. I forget I'm on a forum of engineers and that 0.48 is not 0.50.

Take the advice for what it is, or let the slope fail due to inadequate capacity and explain yourself in court.

If you aren't familiar with the concept then don't speculate.

Seems a bit harsh, Rick. There are legitimate questions.

 

[BridgeSmith]

If we just have a pile of gravel sitting on asphalt, wouldn't we still need to overcome the friction between the gravel & aspalt (or the internal friction of the gravel) in order for it to slide?

It depends on how far you're going to slide it. Visualize if you will, a bulldozer pushing into your pile of gravel, except the pile is 2' high and 50' wide. How far does the bulldozer have to push into the pile before the back of the pile moves? Probably about 30 or 40 feet. Can your house foundation move that far in order to mobilize the resistance of all of that material? The soil inside the foundation is not a solid mass, like the concrete slab, thus the reason we can use the full weight of the slab - if one edge moves, the whole slab moves. Not so for the soil under it. If you push on one side, it doesn't all move; only a small volume near the foundation wall moves, which is why the passive resistance is limited.
If we could do what you're suggesting, the passive resistance on the outside of the foundation would be infinite, but it's not. All you get is the passive resistance of the soil against the foundation wall on the inside, same as you do on the outside, except you can count the weight of the slab in the calculations. Although, if it slides enough to mobilize the passive resistance inside, it will likely lift the slab and (unless it's reinforced) break it.

Rod Smith, P.E., The artist formerly known as HotRod10

 

[BridgeSmith]

...load delivered to the top of the foundation wall will hit the diaphragm there and make it's way through whatever the VLRFS is that stabilizes the diaphragm.

That's a good point. If you're relying on friction between the soil and the bottom of the footing to resist the sliding forces imposed by the retained soil, there will be a large bending moment on the foundation wall, and you'll need more than the typical pinned connection between the top of the foundation wall and the floor diaphragm to keep the foundation wall from rolling over. Either that, or you'll have to extend the footing to the outside and design the foundation as a cantilever retaining wall.

Rod Smith, P.E., The artist formerly known as HotRod10

 

[chris3eb]

@TheRick
I'm not trying to split hairs between 0.48 and 0.50, nor am I disputing that your rule of thumb is a good one - you clearly have more experience in this area than I do.

Your prior post says: "you can see from the images that in a slope you only have roughly half of the resistance." It seems like you are implying there is "roughly half" the resistance because there is one failure surface rather than two. It is that implication that I am questioning.

Below is a picture from my college textbook that shows that shows that on flat ground, a "general shear failure" has a single failure surface.

And here's a figure from a paper that shows that the ratio of the bearing capacity of a foundation on a slope of cohesionless soil can vary widely depending on the slope inclination and the internal friction angle of the soil. The reduction values vary from well above 50% to well below 50%.