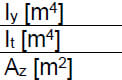bojoka4052
Mechanical
I have three section properties given per meter length as seen below which I need to define a beam element with:
Transverse bending stiffness [m^4/m]
Torsion stiffness [m^4/m]
Transverse shear stiffness [m^2/m]
I can multiply with a certain length to remove the per meter, but after that, where should I place the 3 properties of the beams? I am guessing in one of the red boxes Ive highlighted below since the units coincide, but which ones would it be?
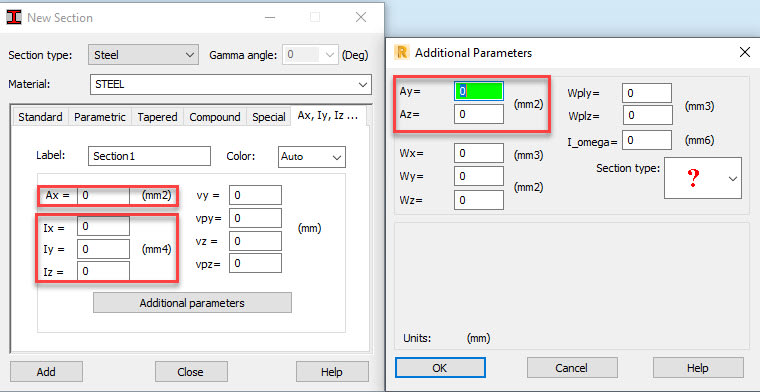
Transverse bending stiffness [m^4/m]
Torsion stiffness [m^4/m]
Transverse shear stiffness [m^2/m]
I can multiply with a certain length to remove the per meter, but after that, where should I place the 3 properties of the beams? I am guessing in one of the red boxes Ive highlighted below since the units coincide, but which ones would it be?