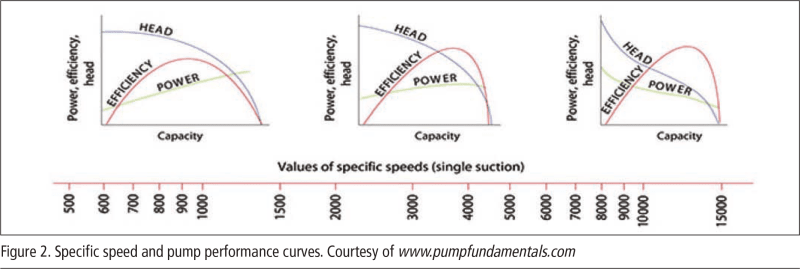
First of all, lets consider a High Nss pump...in the 9000+ range. So it has a steep H-C curve, and more importantly for the purposes of this issue, a high shut off HP. Shut-Off head HP is 2.4 x HP at BEP! Like the right most curve here:
(If this image does not come though, you can view it here: See figure 2 about half way through the article. )
The key characteristic is the pump has high shut off HP. This means you can not just draw the speed torque curve as a parabola.
Why? Because of the affinity laws and the high SO HP. A normal pump (4500 Ns and lower) has peak HP at BEP, or right of BEP. When you start a pump up, you are by definition starting at zero speed. If you have any lift, you are essentially dead heading your pump. Even if you have NO lift, you are still dead heading your pump, because ACCELERATION head creates head above and beyond friction. This pushes you LEFT on any curve at a given speed. But for a normal pump, you don't care, because left on the curve reduces HP. As such, speed torque curves for most "normal" centrifugal pumps are just parabolas, and at full speed, the torque value coincides with the peak HP the pump will run at at full speed (based on a pump and system head curve intersection).
But with a high Nss pump, pushing left on the curve INCREASES HP dramatically. This means your speed torque curve has this S-Curve shape, which is not truly dependent just on speed. It is dependent on speed AND acceleration. The S-T curve is now made up of two parts. One is the paraolic part, as normal. The other is a function of speed AND acceleration. The faster you accelerate the pump, the more the acceleration of the fluid in the pipeline downstream resists, creating a transient acceleration head. This results in the pump seeing higher pressures during acceleration, and thus high loads because the high Ns pump sees HP rise when operated left. The more fluid mass you have to accelerate, the worse the effect. The faster you try to get the pump up to speed, the worse the effect.
As you increase the acceleration time (such as on a VFD), the S-T curve converges to the parabolic case, assuming you are not running the pump against a closed valve, and the system-pump intersection is in a good spot (at or right of the point used to the size the motor)
I have been tasked with creating a mathematical representation of this S-T characteristic due to a field problem where the pump is not starting properly on a reduced voltage starter. If we look at the parabolic case, the pump should start fine based on the motor S-T curve and the reduced voltage sequence being utilized. But we know from field experience, that the pump S-T curve is "worse" than the parabolic case. We just do not know how much worse.
Such a math model would have to take into account the following:
1. The base parabolic speed torque characteristic (T=cN^2...easy)
2. The pump curve and HP curve for any given speed (At a given speed, you need to know the load for a given head)
3. The mass of fluid that needs to be accelerated. This changes over time...which can make things worse. For instance...the worst case would be to start a pump slowly...then try to accelerate from 70% speed to 100% speed almost instantly. This would create a huge load spike. If the mass of the fluid is known, you can calculated the acceleration head for a given rate of acceleration.
Has anyone ever seen any technical guideance (text books, papers, etc) on such an task?

(If this image does not come though, you can view it here: See figure 2 about half way through the article. )
The key characteristic is the pump has high shut off HP. This means you can not just draw the speed torque curve as a parabola.
Why? Because of the affinity laws and the high SO HP. A normal pump (4500 Ns and lower) has peak HP at BEP, or right of BEP. When you start a pump up, you are by definition starting at zero speed. If you have any lift, you are essentially dead heading your pump. Even if you have NO lift, you are still dead heading your pump, because ACCELERATION head creates head above and beyond friction. This pushes you LEFT on any curve at a given speed. But for a normal pump, you don't care, because left on the curve reduces HP. As such, speed torque curves for most "normal" centrifugal pumps are just parabolas, and at full speed, the torque value coincides with the peak HP the pump will run at at full speed (based on a pump and system head curve intersection).
But with a high Nss pump, pushing left on the curve INCREASES HP dramatically. This means your speed torque curve has this S-Curve shape, which is not truly dependent just on speed. It is dependent on speed AND acceleration. The S-T curve is now made up of two parts. One is the paraolic part, as normal. The other is a function of speed AND acceleration. The faster you accelerate the pump, the more the acceleration of the fluid in the pipeline downstream resists, creating a transient acceleration head. This results in the pump seeing higher pressures during acceleration, and thus high loads because the high Ns pump sees HP rise when operated left. The more fluid mass you have to accelerate, the worse the effect. The faster you try to get the pump up to speed, the worse the effect.
As you increase the acceleration time (such as on a VFD), the S-T curve converges to the parabolic case, assuming you are not running the pump against a closed valve, and the system-pump intersection is in a good spot (at or right of the point used to the size the motor)
I have been tasked with creating a mathematical representation of this S-T characteristic due to a field problem where the pump is not starting properly on a reduced voltage starter. If we look at the parabolic case, the pump should start fine based on the motor S-T curve and the reduced voltage sequence being utilized. But we know from field experience, that the pump S-T curve is "worse" than the parabolic case. We just do not know how much worse.
Such a math model would have to take into account the following:
1. The base parabolic speed torque characteristic (T=cN^2...easy)
2. The pump curve and HP curve for any given speed (At a given speed, you need to know the load for a given head)
3. The mass of fluid that needs to be accelerated. This changes over time...which can make things worse. For instance...the worst case would be to start a pump slowly...then try to accelerate from 70% speed to 100% speed almost instantly. This would create a huge load spike. If the mass of the fluid is known, you can calculated the acceleration head for a given rate of acceleration.
Has anyone ever seen any technical guideance (text books, papers, etc) on such an task?
