ElyasCivil
Civil/Environmental
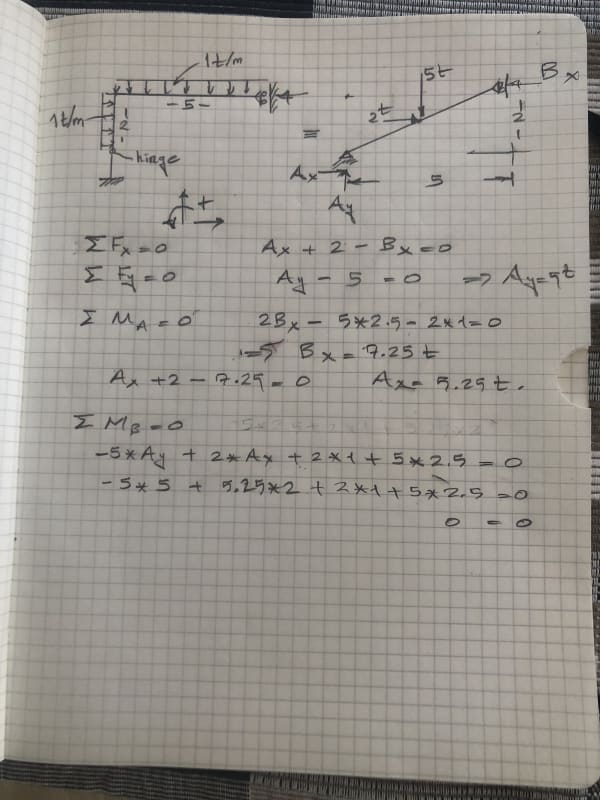
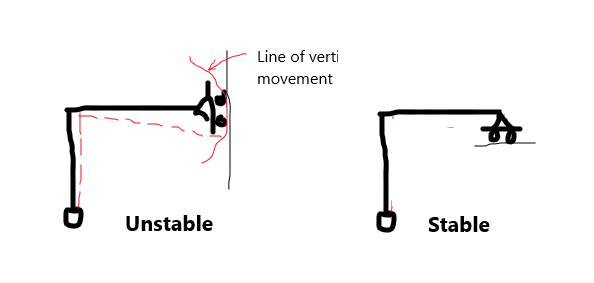
Hello everyone, I have a question regarding the stability of a frame:
I may be wrong but from what I have learned to check for stability given a determinant system you must control two things:
1) Not all reactions forces are parallel or concurrent. (This frame satisfies this rule)
2) Rigid bodies are connected by 3 non-parallel and non-concurrent constraints. (I am not sure about this, from what I see the frame is composed of two rigid bodies connected by a hinge and the hinge provides 2 constraints (one in x and one in y direction)
So I would conclude this frame is determinant and NOT STABLE. Im I wrong?
Thank you very much I am attaching a picture for your review
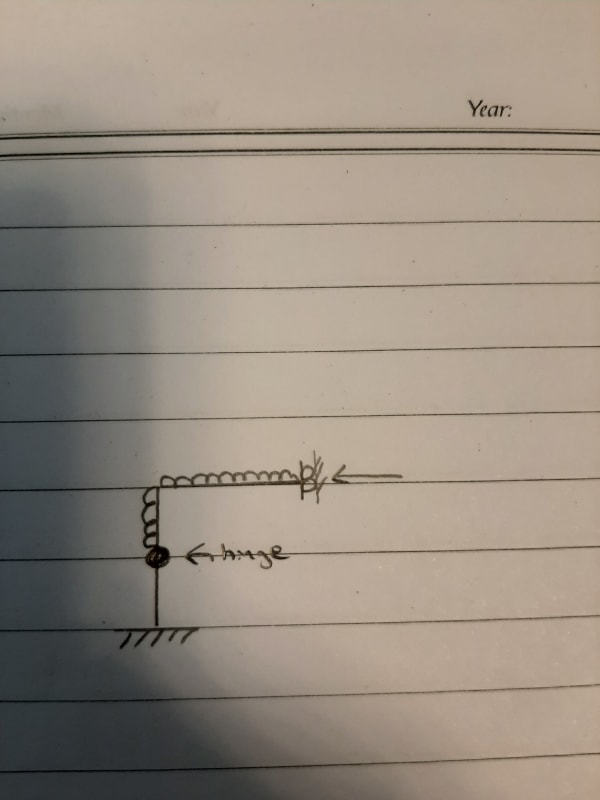
I may be wrong but from what I have learned to check for stability given a determinant system you must control two things:
1) Not all reactions forces are parallel or concurrent. (This frame satisfies this rule)
2) Rigid bodies are connected by 3 non-parallel and non-concurrent constraints. (I am not sure about this, from what I see the frame is composed of two rigid bodies connected by a hinge and the hinge provides 2 constraints (one in x and one in y direction)
So I would conclude this frame is determinant and NOT STABLE. Im I wrong?
Thank you very much I am attaching a picture for your review