greenimi
Mechanical
- Nov 30, 2011
- 2,259
Question for the group":
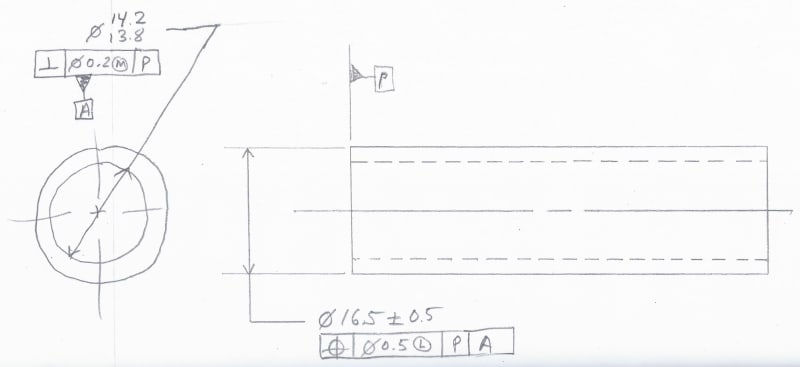
(Ref: ""maximum wall thickness at one spot" vs. "maximum consistent wall thickness." from a previous discussion)
How the stackup -minimum and maximum wall distance- change (if it does ) , IF I would say that:
X maximum = maximum possible distance that can ever happen in a single cross section for cases.
x minimum = minimum possible distance that can ever happen in a single cross section for cases.
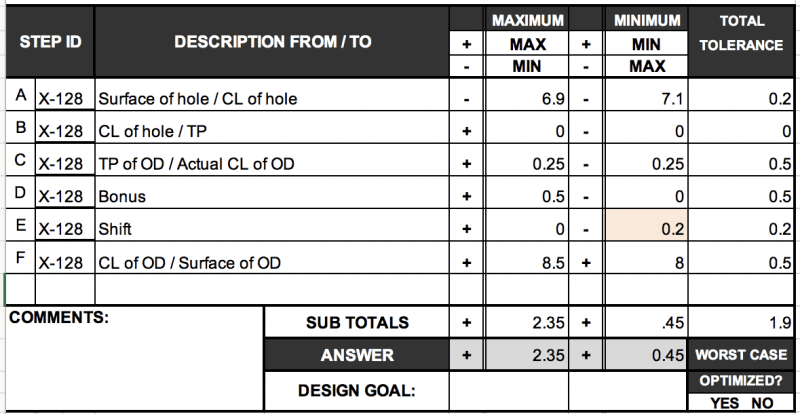
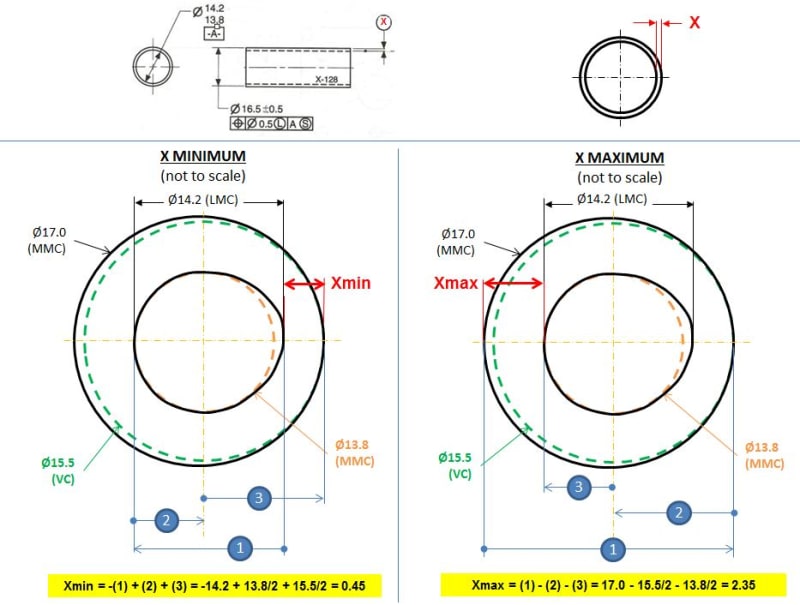
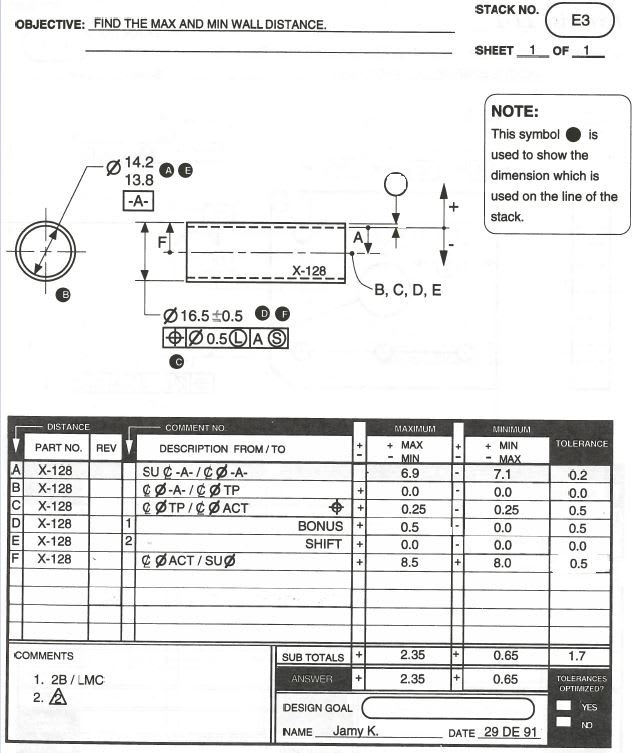
Will those two values of 2.35 and 0.65 for the maximum wall distance and minimum wall distance respectively, change with my above adjustment?
If yes, what would be the "new" values for X maximum and x minimum?
Thank you very much
(Ref: ""maximum wall thickness at one spot" vs. "maximum consistent wall thickness." from a previous discussion)
How the stackup -minimum and maximum wall distance- change (if it does ) , IF I would say that:
X maximum = maximum possible distance that can ever happen in a single cross section for cases.
x minimum = minimum possible distance that can ever happen in a single cross section for cases.
Will those two values of 2.35 and 0.65 for the maximum wall distance and minimum wall distance respectively, change with my above adjustment?
If yes, what would be the "new" values for X maximum and x minimum?
Thank you very much