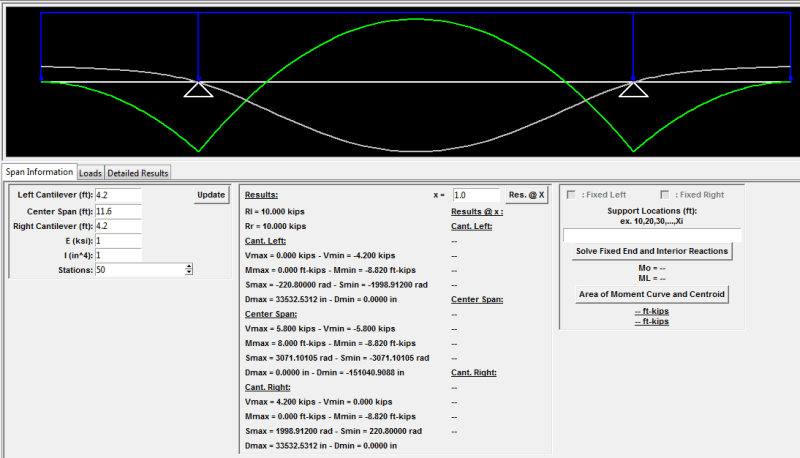
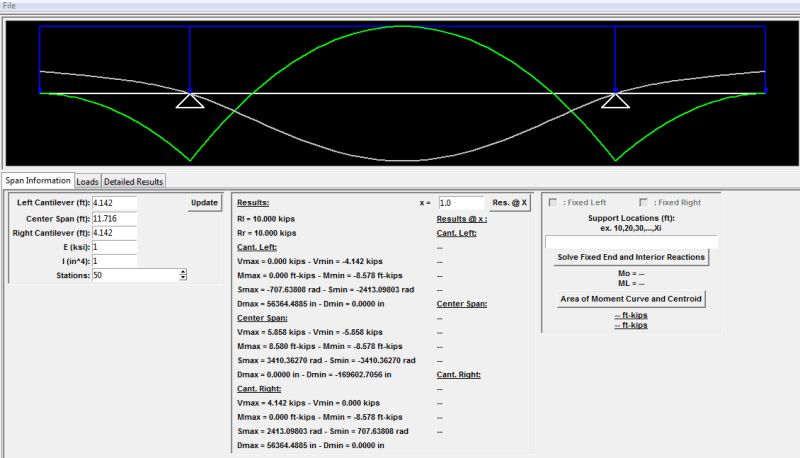
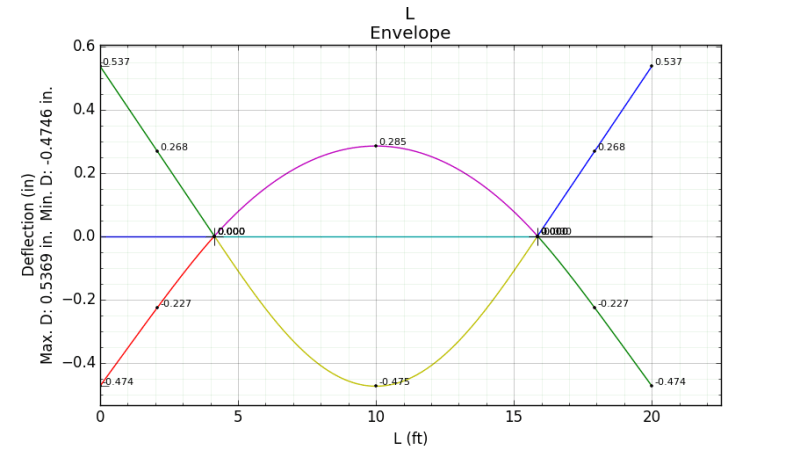
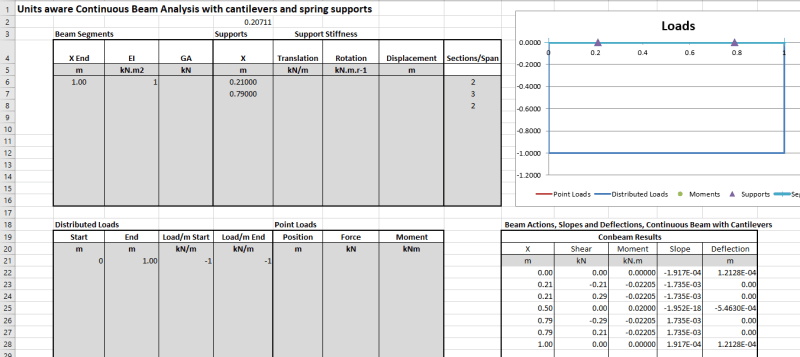
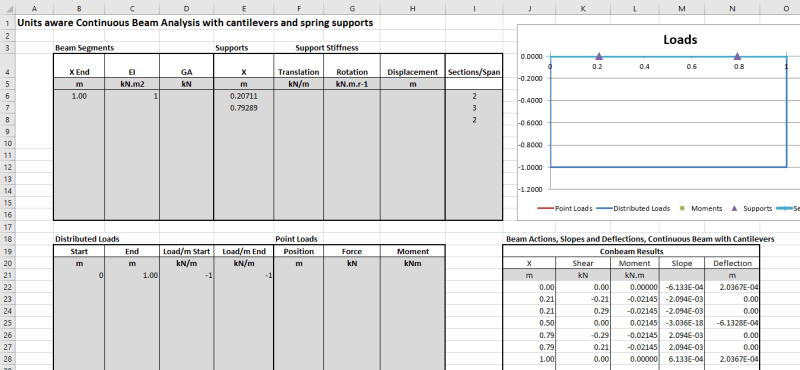
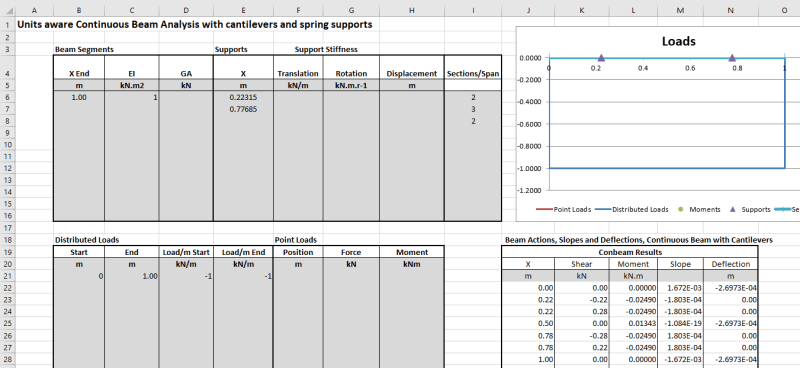
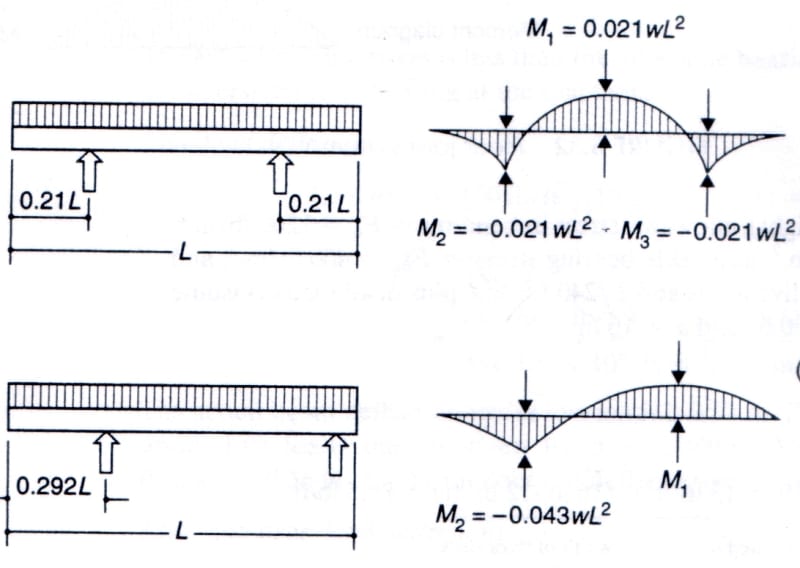
I thought about applying double cantilevering to minimize the material for a small structure, but I don't seem to find a standard formula for the deflection of this beam (see figure - I refer to the case on top although if formulae for the maximum deflections for both cases are available I would appreciate having them both)
Thank you!
Thank you!