Dear,
I want to make a state space model of a simple mass spring damper system with a base excitation as shown in the figure below.
The equation of motion is:
mx'' + bx' + kx = ky + by'
How can I write this in state space (A,B,C,D) format? I have difficulties with finding the B matrix.
y(t) = Y sin (Wt)
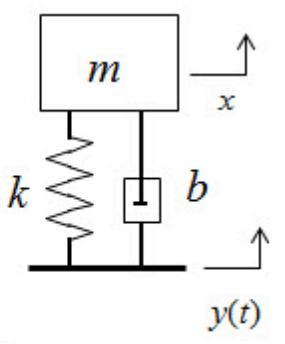
I want to make a state space model of a simple mass spring damper system with a base excitation as shown in the figure below.
The equation of motion is:
mx'' + bx' + kx = ky + by'
How can I write this in state space (A,B,C,D) format? I have difficulties with finding the B matrix.
y(t) = Y sin (Wt)

