Static or Stagnation Pressure for Evaluating Fire Sprinkler Minimum Operating Pressure? 6

[az5333]

Hi fellow members.

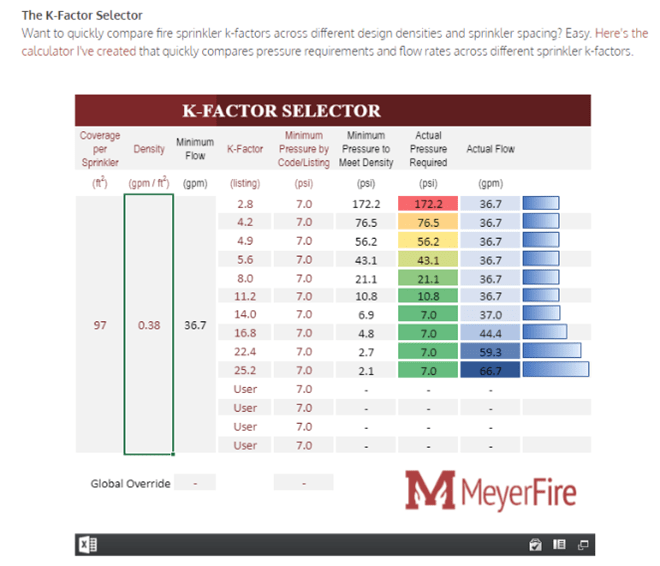
I am working on designing a wet pipe fire sprinkler system for a small room and I am using "Fluidflow software" to perform the hydraulic calculations. I am stuck at a very simple concept but I need your help in clarifying that. Sprinkler manufacturers recommend that the sprinkler operate at or above a minimum residual (flowing) pressure of 7 psi. Now my question is, when we look at the pressure available at the sprinkler head, do I look at the stagnation pressure or the static pressure? For example, for one of the most remote sprinklers, the stagnation pressure is coming out to be 7.72 psig and static pressure is 2.35 psig. Should I be comparing the stagnation pressure (7.72 psig) to the min. requires pressure (7 psig)? Appreciate the help and support.

 

[bimr]

Albeit the risk of being proved completely wrong by going against the tide versus all the way more knowledgeable colleagues here, I'll state that in my opinion the "right" pressure to use for the calculation using the "Sprinkler equation" that fire systems love to use is the stagnation pressure in lieu of the static pressure.

Stagnation pressure is usually what is implied when just the term “pressure” is used in discussions.

The difference between Stagnation and Static Pressure is the Dynamic Pressure, which represents the kinetic energy of the flowing fluid. Dynamic pressure is a function of the fluid velocity and its density.

In the example with the 4 inch pipe, 700 gpm results in a fluid velocity of 17.6 ft/sec, a dynamic pressure of 2.1 psi, and static pressure of 97.9 psig, and stagnation pressure of 100 psig.

The Stagnation Pressure is the sum of the Static Pressure and the Dynamic Pressure, also shown in the equation below:

Ptotal = Pstatic + Pdynamic

For many liquid applications, the pipelines are sized to ensure low fluid velocities to reduce the head loss and pressure drop for a given flow rate, resulting in a small value of dynamic pressure. Also, because of the accuracy and scale of the instrument used to measure the pressure, the distinction between total (stagnation) and static pressure may be neglected. In the example above, the difference between stagnation pressure and static pressure is just 2% when the fluid is flowing at 17 ft/sec which is a typical velocity in fire systems.

Link

 

[bimr]

Thanks for your responses. As per the maximum sprinkler coverage areas per sprinkler for our design (96.7 ft2) and the design discharge density of 0.38 gpm/ft2 per sprinkler, the minimum flowrate that is needed per sprinkler is 36.7 gpm. Therefore, in the software, I am setting the residual pressure (at the base of the riser) such that this minimum flowrate is achieved per sprinkler. During this process, I also am checking if the minimum operating pressure condition is met (i.e. 7 psig). I have used K11.2 SC/SR sprinklers for the application. I have used "Extra Hazard Group 2" design curve from NFPA 13 (0.38 gpm/ft2 over 3000 ft2) and then reduced the area by 25% considering the provision given in NFPA 13 section 19.3.3.2.7 with a final selected design area of 2250 ft2. The total number of sprinklers in design area (active sprinklers) are coming out to be 31. Hopefully this clarifies the overall design scenario I am considering for the application. Currently, my residual pressure at the base of riser is coming out to be 38 psig with these calculations as per the software. We are scheduled for a hydrant flow test with the city in a couple of weeks, but all we have so far is the static pressure at the base of the riser and that is 43 psig. So things are definitely not looking good. That is why I was trying to clarify if it is the stagnation or the static pressure I have to consider, as stagnation pressure values gave me quite a relief in terms of required residual pressure. Please let me know if you think I need to change my approach or re-visit the design parameters.

The online calculator from Meyer Fire:

Using the 11.2 K-Factor, the calculator shows you need 10.8 psi at the sprinkler to obtain the desired flow.

If you have the 43 psi at the farthest sprinkler, your system should be acceptable.

Link

 

[bimr]

Some fire protection design standards from axaxl:

Link 1

Link 2

Link 3

 

[pierreick]

Hi,
let you consider the link underneath where you can find a methodology and a software .

https://www.canutesoft.com/how-to-calculate-a-fire-sprinkler-system.html

Note:
To me the most important is to get a registered contractor to perform the calculation , knowledgeable about the codes , the requirement of the administration (safety bureau, fire fighting brigade ,) . If you fail to do so , you could have a long delay to obtain your operation license. This is based on 20 years experience in Asia .

Good luck
Pierre

 

[danschwind]

I have the same opinion as bimr. Stagnation pressure should be the pressure figure unless stated otherwise.

Daniel
Rio de Janeiro - Brazil

 

[1503-44]

Currently, my residual pressure at the base of riser is coming out to be 38 psig with these calculations as per the software. We are scheduled for a hydrant flow test with the city in a couple of weeks, but all we have so far is the static pressure at the base of the riser and that is 43 psig.

Definitely not a good sign that there is only 43 static. Stagnation pressure is very likely to be lower than 38.

But if you designed a tree system with a proper cross main, you might do better than 38 required at the riser. Have you tried that yet? Every psi will count.

 

[1503-44]

I'm trying to duplicate your results, but I don't see some critical information.
How far apart are the sprinklers.
C factor of pipe.

So far I used 10ft between sprinklers,
C = 140
5 ft to the cross tee
50ft of 3" pipe
35ft 4" pipe
And get 43 psig, but at the beginning of the branch at the cross connection.
There is still more pipe to go.
12 ft down is another 5 psi
And I do not yet include fitting losses.

 

[PEDARRIN2]

1503-44

If C is the friction factor used, most of the ones I have seen for wet pipe have been 120 for black steel.

 

[1503-44]

Thanks. Yes I know the C values. Where does az533 say he has used 120?
Where does he say he has used a material with a known C value at all?

I am trying to show az533 how close his design is to failing, so I used C=140 so my example would have a lot less pressure loss. But thanks, he might not have noticed that.

I have also worked out two example configurations.
One example uses a configuration similar to az5333's "bush" configuration.
The other example uses a tree configuration, similar to the one I posted above.
Both examples have the same K=11.2 sprinklers at 10ft C/C.
Both examples cover a grid area of 5600ft2. 40' x 140'
Ex 1 has 4 branches 10' apart =30' and are each 130ft long. 13 sprinklers at 10' c/c.
Ex 2 has 26 branches, 15' long extending either side of a central 130ft long cross main. 2 sprinklers ea. At 10' c/c.
I have ignored all fittings for now.
I have kept velocities <30 fps.

Presuming I did this correctly.
Example 2, the tree configuration is far more efficient.
It needs 20% less flow. Important if supplied from a tank get, or if water is pumped.
It needs 8% less pressure. Very important with low residual pressure.
It has 7% less max velocity. Probably not significant.
And uses 60% less weight of pipe than a bush configuration.
Very significant.
It would appear that using short branch strings with few sprinklers are more efficient.
Minimising use of lots of smaller bore pipe pays off by collecting flow and quickly getting it moving through larger more efficient diameters.

I have not found any errors in my configuration analysis.
I think it shows just how bad some configurations can be.

 

[GospodinSneg]

Oh boy, I'm late to this party. I made an account for this.

My career is what you're doing right now; fire sprinkler design. I'm currently at NICET level II, and will be eligible for III this year.

Bluntly, you're in over your head here and you need to have someone else do this or prepare for weeks of reading NFPA 13 and probably use different software or break out some spreadsheets and graph paper.

You are not limited to 8 heads per branch, nor any size requirements except that 1 inch pipe is the minimum size except in rare edge cases, none of which you'll find in EHII. That is the old pipe schedule system that served for uncalculated systems, which are no longer allowed to be installed. If you see a sprinkler system following that sizing and it's 30+ years old, you may be looking at a schedule system.

The 7psi minimum is for any sprinkler, meaning if it's in a 24 ft^2 light hazard closet, required operating pressure is 7psi regardless of coverage area and density showing that 2.4gpm is required and therefore pressure will be almost negligible.

For such a case, flow is also adjusted accordingly, and the head would operate based on Q=K*sqrtP

Overall, hydraulic calculation is not going to be well served or accurate by your chosen method.

To start, the table with area/density requirements is not your only limitation. I haven't taken a thorough look but there are stringent requirements for how that area is to be determined, not just its size.

Secondly, there are two pressures a sprinkler system cares about: static and residual. That being pitot tube pressure at 0 flow and available pressure at flow demand condition.

(You can use normal pressure calculations based on the velocity pressure formula found in NFPA 13, but this is extremely rarely practiced.)

Additionally, calculations are near recursive processes due to how they are performed.

You will start your calcs backwards, at the end head of your remote area, using Hazen-Williams. It's not enough to say "x gpm per y sprinklers" and run.

I'll make the math easier for myself and call your end head 100ft^2 at .4gpm/ft^2. Its flow is 40gpm, and with 11.2K, pressure required is nearly 12.8psi while flowing. Calculate pressure loss through the pipe to the next flow device, size change, or C factor change, adding equivalent lengths.

Next head, add another 40gpm, calc a now 80gpm of flow to the next change, and so on.

13 heads is 520gpm at the main/branch line intersection of your end line, and if that pipe isn't huge I shudder to consider how much you're losing per foot. Your end head pressure plus the sum of all the friction/elevation losses up to this point is now your overall pressure demand at that 520gpm.

Calc flow demand through main back towards riser to next branch line.

Now, if the branch line is identical, you'd be fine to assume its calculated demand is 520gpm at the same pressure. However, your overall demand is slightly higher due to demand from the friction loss across the main, and NFPA requires you to balance the pressure demand at that intersection to within 0.5psi, so if there is a larger discrepancy, you must adjust the flows of the heads on that line until the pressure demand is within 0.5 psi of demand 1 (branch line 1 + cross main friction loss). Your new demand let's call an even 1100 because I'm not going to actually go through that process manually.

(The other variable you can control to inflate pressure demand at an intersection is pipe size downstream. You can try that but loss is drastically different on the smaller diameters at the flows you've got.)

Calc 1100gpm worth of friction loss down the main to the third branch line. Repeat the balancing procedure for branch line 3. Note that because your loss through the main is now 1100 you're losing more to friction loss from line 2 to 3 than 1 to 2, and balancing line 3 will have accordingly increased overflow.

Repeat until you reach either base of riser, or preferably a fire hydrant or other water supply connection where a flow test was performed. Add outside hose allowance here.

Bear in mind that elevation loss/gain is calculated from reference point to reference point, so while this isn't the case for your building, branch lines on a pitch with one side going up from the main and the other going down will induce massive overflow at intersections unless you adjust branch line sizes accordingly.

If this system is existing, my recommendation would be to attempt a calculation based on relocating the main to split the branch lines with 6/7 heads on each side, setting the main closer to the 7 head side than the 6 to reduce overflow. From there, if it didn't work you'd be looking at either increasing the main/riser size, gutting the branch lines to increase their sizes, or making a grid system probably. Either that or estimating if adding a fire pump and its corresponding code parsing is cheaper.

Last point: you can eliminate one fitting serving the sprinkler (is, the tee or reducer the head screws into) per head from equivalent length calculations. So if the head screws directly into the tee you can omit that tee, but that still won't do a whole lot for you.

Best of luck, although I assume that by now this problem has reached a conclusion.