Caspers6011
Student
I'm hoping someone can help me out with the following question
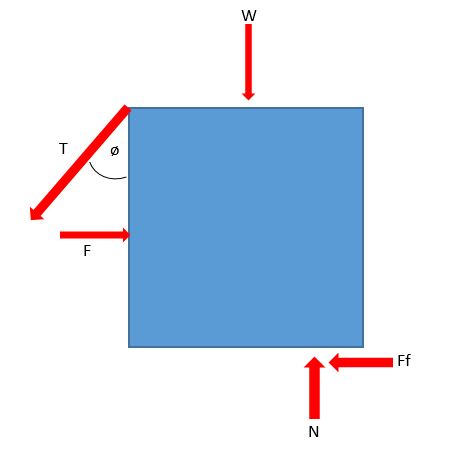
A shipping container has a force applied to the side of it. If a nonrigid chain is tied from the top of the container to an anchor in the ground, how much tension much the chain be able to withstand in order to prevent the container from moving.
Weight (W)= 1702 kg
Force (F)= 47423 N
Angle of T = 20 degrees
Coefficient of Friction=0.3
The box has dimensions of 2.436m x 2.436m
A shipping container has a force applied to the side of it. If a nonrigid chain is tied from the top of the container to an anchor in the ground, how much tension much the chain be able to withstand in order to prevent the container from moving.
Weight (W)= 1702 kg
Force (F)= 47423 N
Angle of T = 20 degrees
Coefficient of Friction=0.3
The box has dimensions of 2.436m x 2.436m




![[pipe] [pipe] [pipe]](/data/assets/smilies/pipe.gif) Tipping action was neat... I'd never thought about it until engineering classes... then, for a few weeks afterwards, whenever I came across an object that could tip, I checked out the location of the horizontal force to see if it worked... I was pleasantly surprised. Thanks, guys... a neat topic.
Tipping action was neat... I'd never thought about it until engineering classes... then, for a few weeks afterwards, whenever I came across an object that could tip, I checked out the location of the horizontal force to see if it worked... I was pleasantly surprised. Thanks, guys... a neat topic.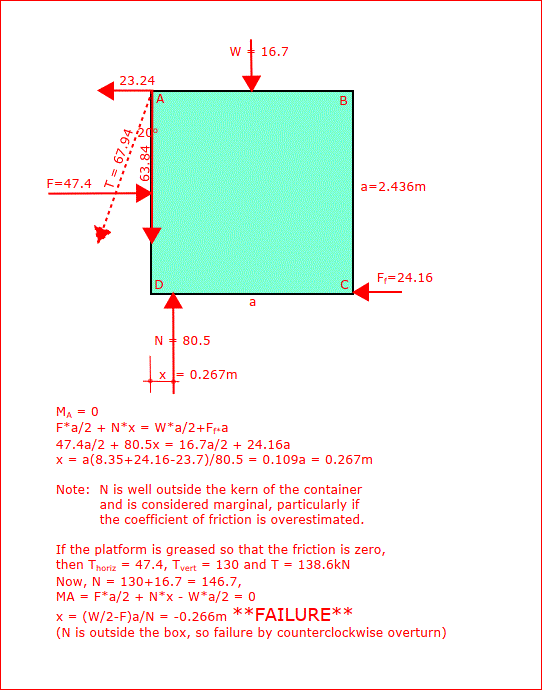
![[thumbsup] [thumbsup] [thumbsup]](/data/assets/smilies/thumbsup.gif)