Pavan Kumar
Chemical
- Aug 27, 2019
- 397
Hi All,
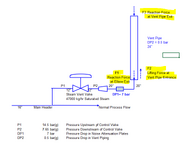
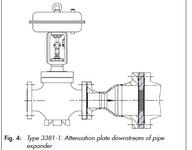
I want to calculate the reaction force at the elbow exit(F1) and vent pipe exit(F3) for a Steam Vent Control Valve that has been sized to vent excess steam pressure. It has been sized to vent the full boiler load as the worst-case. At this flow (47000 kk/hr), the pressure upstream of the control valve is 14.5 bar(g) and the pressure downstream of the control valve is 7.62 bar(g) ( 0.5 bar in the piping (assumed) and 7.12 bar in the noise attenuation plates given by the Control valve vendor). I am trying to calculate the reaction force using ASME B31.1(2020) Non Mandatory Appendix II -Section II-2.2.1 gives a methodology for a PSV with an Elbow discharge ( with and without vent pipe).
I want calculate the following for my application and want to know if the method given in ASME B31.1 can be applied or not. If not what is the correct way. My system sketch is copied below.
A Thread on this forum discussed a little bit on this topic but for a PSV with silencer in the downstream. If this can be applied I want to know how to correctly estimate the equivalent length for the silencer.
https://www.eng-tips.com/threads/silencer-sizing-and-psv-outlet-piping.200194/
1. Pressure at Control Valve Exit,. P1a
2. Pressure at Elbow Exit, P1
3. Velocity at Elbow Exit, V1
4. Reaction Force at Elbow Exit, F1
5. Pressure at Vent Pipe Exit, P3
6. Reaction Force at Vent Pipe Exit, F3
7. Lifting Force at Vent Pipe Entrance, F2.
Thanks and Regards,
Pavan Kumar
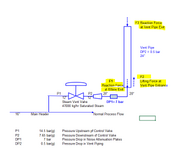
I want to calculate the reaction force at the elbow exit(F1) and vent pipe exit(F3) for a Steam Vent Control Valve that has been sized to vent excess steam pressure. It has been sized to vent the full boiler load as the worst-case. At this flow (47000 kk/hr), the pressure upstream of the control valve is 14.5 bar(g) and the pressure downstream of the control valve is 7.62 bar(g) ( 0.5 bar in the piping (assumed) and 7.12 bar in the noise attenuation plates given by the Control valve vendor). I am trying to calculate the reaction force using ASME B31.1(2020) Non Mandatory Appendix II -Section II-2.2.1 gives a methodology for a PSV with an Elbow discharge ( with and without vent pipe).
I want calculate the following for my application and want to know if the method given in ASME B31.1 can be applied or not. If not what is the correct way. My system sketch is copied below.
A Thread on this forum discussed a little bit on this topic but for a PSV with silencer in the downstream. If this can be applied I want to know how to correctly estimate the equivalent length for the silencer.
https://www.eng-tips.com/threads/silencer-sizing-and-psv-outlet-piping.200194/
1. Pressure at Control Valve Exit,. P1a
2. Pressure at Elbow Exit, P1
3. Velocity at Elbow Exit, V1
4. Reaction Force at Elbow Exit, F1
5. Pressure at Vent Pipe Exit, P3
6. Reaction Force at Vent Pipe Exit, F3
7. Lifting Force at Vent Pipe Entrance, F2.

Thanks and Regards,
Pavan Kumar