Hi guys. I have a steel beam that is loaded with distributed load + concentrated - point loads at the bottom flange.
So in bottom flange there will be stresses from bending of the beam because of distributed load (qd) + thre will be stress perpendicular to that because of point load acting on the edge of a bottom flange. I was thinking about using Von Misses criteria for this. The problem is it has been ages since I have used this. I forgot a lot. is it allrigt to use 'plane' equation for this and Gyy as G1 and Gxx as G2?
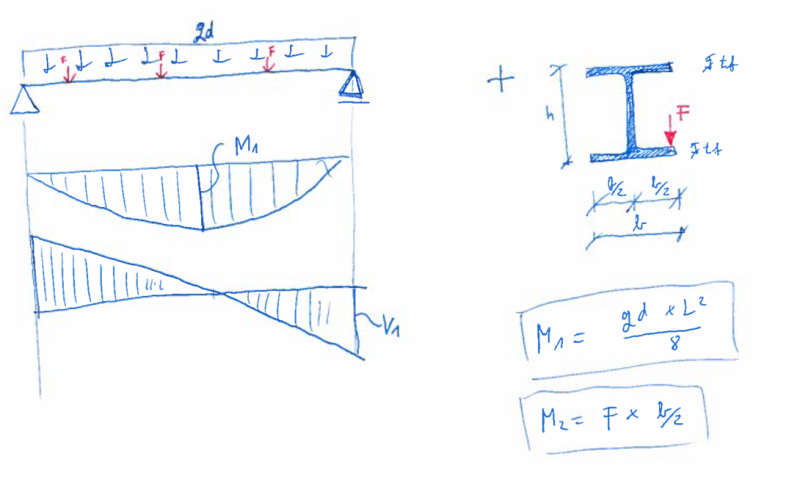
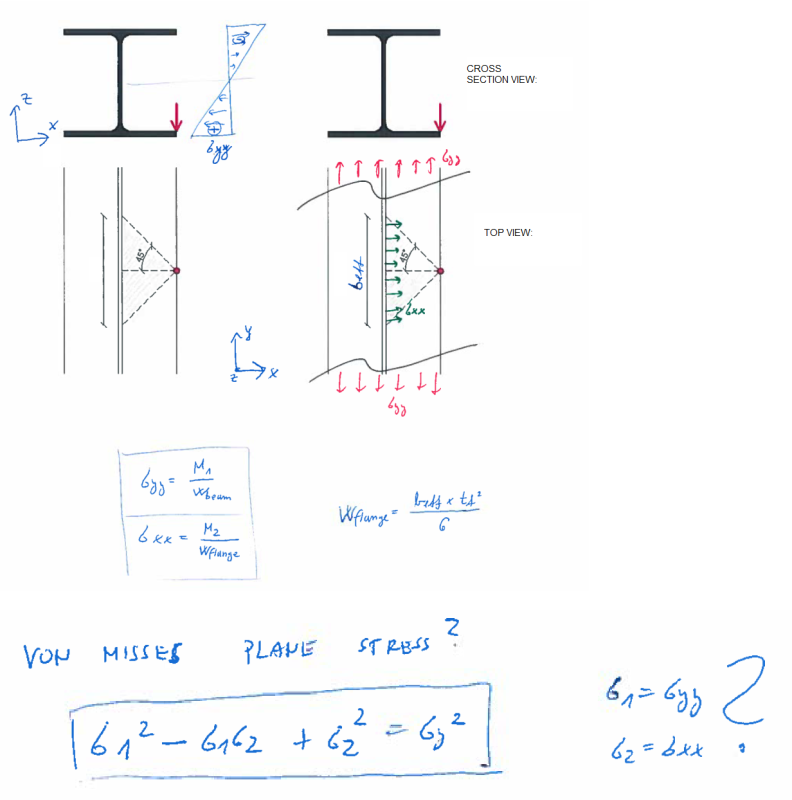
So in bottom flange there will be stresses from bending of the beam because of distributed load (qd) + thre will be stress perpendicular to that because of point load acting on the edge of a bottom flange. I was thinking about using Von Misses criteria for this. The problem is it has been ages since I have used this. I forgot a lot. is it allrigt to use 'plane' equation for this and Gyy as G1 and Gxx as G2?


