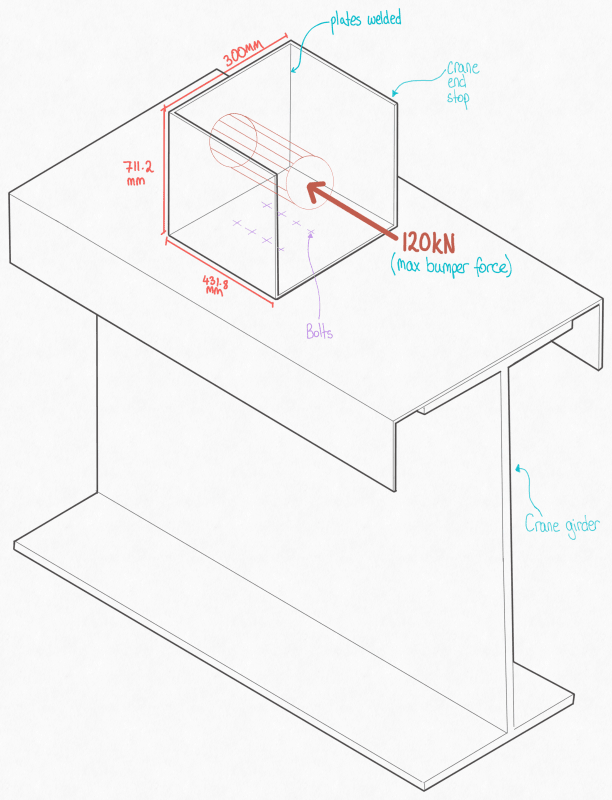
Hi there,
I'm working on the design of a 3/4" thick steel plate that has fixed supports on 3 sides and is free on 1 side. There is a load of 120kN applied to the plate and the plate has the dimensions as shown below :
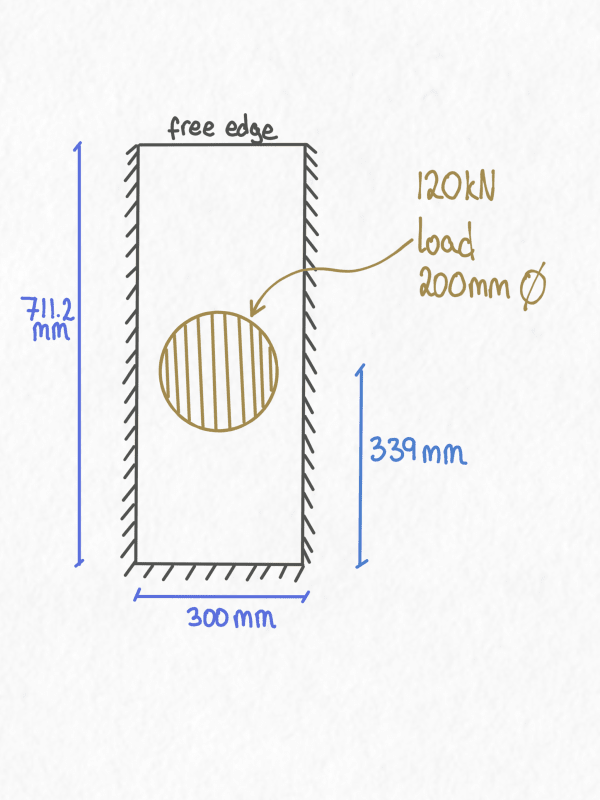 .
.
I'm trying to figure out how to analyse this.
This passes fine if analysed as a simply supported beam spanning in the short direction. Although I'm not sure if that is unconservative?
I looked in to Roark's stress tables but the only suitable case appears to be this one, which is conservative as it's simply supported instead of fixed (which is fine). However, it only considers a UDL load acting on the entire plate as shown below :
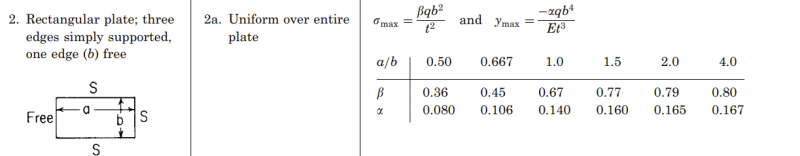
Is there a way that I can convert the concentrated load into a UDL acting on the entire plate.
My first attempt was to take the 120kN load and apply that over the area of the circle which has a diameter of 200mm. However, this resulted in a pressure of 3.82 MPa (120,000/31415.93), which doesn't work and seems a bit too conservative.
Can I take the point load and spread it over the plate area so : 120000/(711*300) = 0.57 MPa? Or will this concentrated load case not work with the Roark tables?
If not, would the initial approach designing as a simply supported beam spanning in the short direction be a reasonable approach? Designing as a beam that is 3/4" deep and 300mm wide with a 120kN point load in the center. The ratio of plate lengths is 711.2/300 = 2.37
I'm working on the design of a 3/4" thick steel plate that has fixed supports on 3 sides and is free on 1 side. There is a load of 120kN applied to the plate and the plate has the dimensions as shown below :

I'm trying to figure out how to analyse this.
This passes fine if analysed as a simply supported beam spanning in the short direction. Although I'm not sure if that is unconservative?
I looked in to Roark's stress tables but the only suitable case appears to be this one, which is conservative as it's simply supported instead of fixed (which is fine). However, it only considers a UDL load acting on the entire plate as shown below :
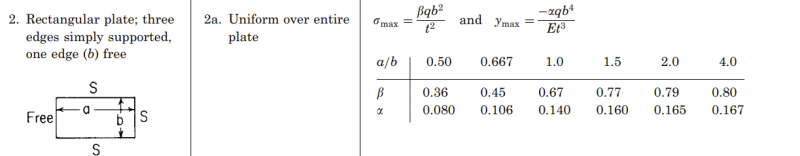
Is there a way that I can convert the concentrated load into a UDL acting on the entire plate.
My first attempt was to take the 120kN load and apply that over the area of the circle which has a diameter of 200mm. However, this resulted in a pressure of 3.82 MPa (120,000/31415.93), which doesn't work and seems a bit too conservative.
Can I take the point load and spread it over the plate area so : 120000/(711*300) = 0.57 MPa? Or will this concentrated load case not work with the Roark tables?
If not, would the initial approach designing as a simply supported beam spanning in the short direction be a reasonable approach? Designing as a beam that is 3/4" deep and 300mm wide with a 120kN point load in the center. The ratio of plate lengths is 711.2/300 = 2.37