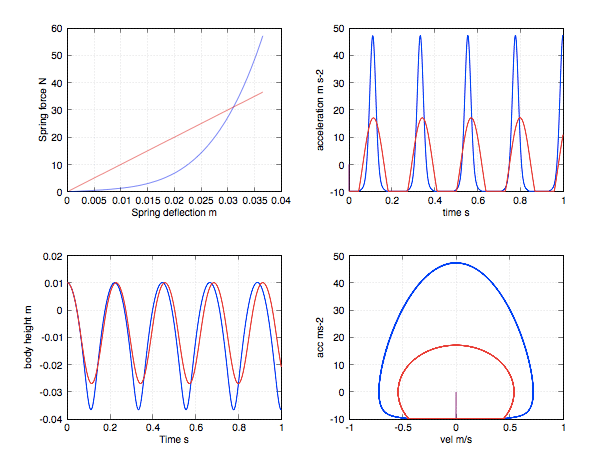
Hello everyone. I am familiar with simple mechanical system modeling using springs and dashpots, like below photos, in a transfer function:
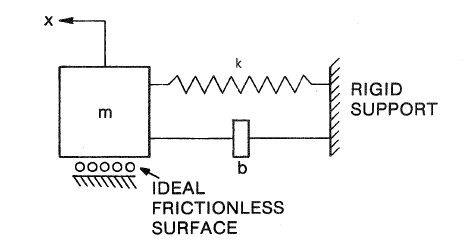
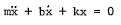
...but can anyone point me in the correct direction for modeling this system with a rubber isolator?
I cannot simply model isolators as springs/dashpots because polymer materials like rubber are nonlinear in compression/tension and have varying properties based on different frequencies.
What is a common technique to predict response of an isolator based on geometry and composition?
I'm basically looking for some book recommendations or input on where to start researching.
Thanks!

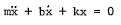
...but can anyone point me in the correct direction for modeling this system with a rubber isolator?
I cannot simply model isolators as springs/dashpots because polymer materials like rubber are nonlinear in compression/tension and have varying properties based on different frequencies.
What is a common technique to predict response of an isolator based on geometry and composition?
I'm basically looking for some book recommendations or input on where to start researching.
Thanks!