stiffness of RC beam - internal forces

[gmd255]

Hello.
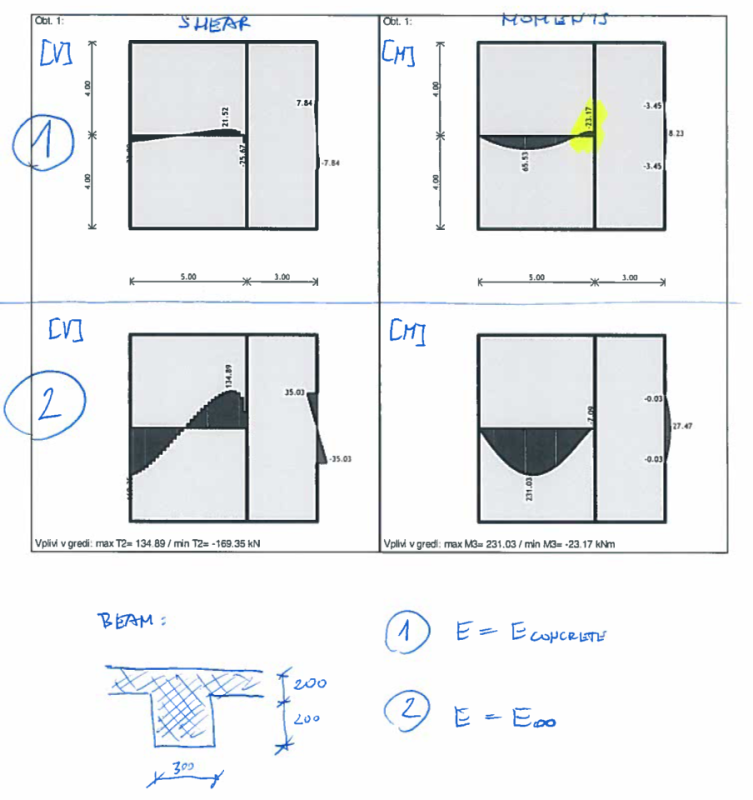
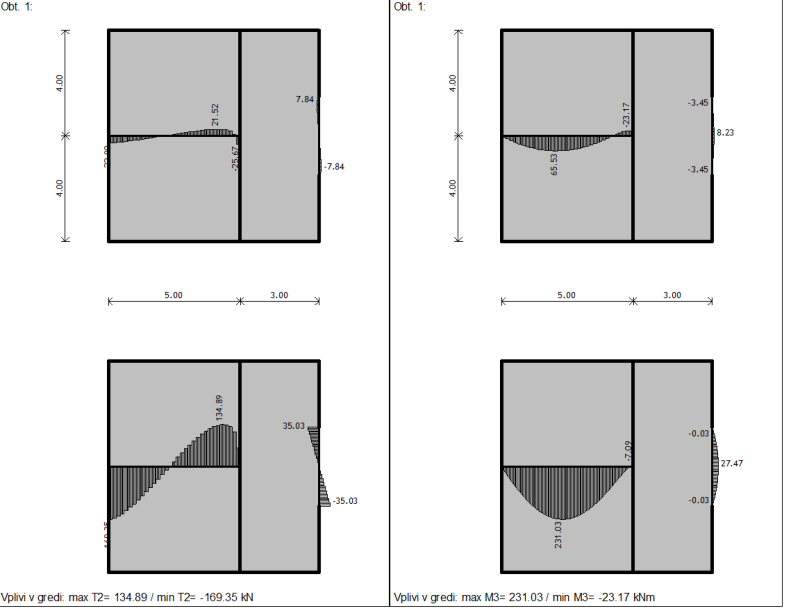
I d like to hear some explanation why stiffness of a beam has such influence on internal forces (shar, bending moments) of the beam. In my case I have 200 mm RC slab with a design load of 20 kN/m2.

In case #1 the stiffness of a beam is equal: EI (where E is modulus of elasticity for concrete and I is a moment of inertia)

In case #2 I choose E to be infinite value so my beam is infinitely stiff.
In this case it acts as a wall/support.

Im wondering why there is such a large difference in internal forces in the beam between #1 and #2?

When you model a beam that is partly integrated in a slab, do you use #1 or something between case #1 and #2?

Im asking this because If I choose model #1 then my internal forces are pretty small. Also I get negative moment above support (marked yellow in picture bellow).

Id like to know whats the bet way to model this since I often get pretty small and 'unclear' forces when choosing case #1
Also slab forces are different for case #1 and #2 which is logical...

 

[gmd255]

Im posting a better version:

 

[gmd255]

Anyone?

 

[hokie66]

This question is fundamental to understanding how structures work. A search of the site results in a number of similar queries, one of which is linked here.

thread507-422787