Mateus_R
Mechanical
- Mar 15, 2018
- 48
Hello everyone,
I'm analyzing how to measure the strains and obtain the stresses at a pipe using a strain gage (measuring circumferential and longitudinal strain with a rosette), and I was informed that the relation between radial strain and the other two components is the following one:
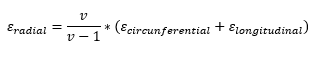
Someone knows from where this relation comes from and how to derive it?
Thank you.
I'm analyzing how to measure the strains and obtain the stresses at a pipe using a strain gage (measuring circumferential and longitudinal strain with a rosette), and I was informed that the relation between radial strain and the other two components is the following one:
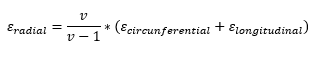
Someone knows from where this relation comes from and how to derive it?
Thank you.